Выпуклость и перегибы графика функции
Графиком функции  , заданной на множестве
, заданной на множестве  , называют множество точек плоскости с координатами
, называют множество точек плоскости с координатами .
.
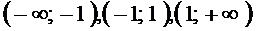 , если касательная к графику в любой точке этого промежутка расположена ниже графика. Если касательная расположена выше графика, то график называют выпуклым вверх. Точка, в которой график меняет направление выпуклости, называется точкой перегиба.
, если касательная к графику в любой точке этого промежутка расположена ниже графика. Если касательная расположена выше графика, то график называют выпуклым вверх. Точка, в которой график меняет направление выпуклости, называется точкой перегиба. Если на промежутке 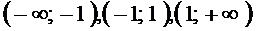 вторая производная
вторая производная  положительна, то график является выпуклым вниз на этом промежутке. Если
положительна, то график является выпуклым вниз на этом промежутке. Если  на промежутке
на промежутке 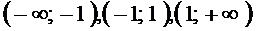 , то график является выпуклым вверх на промежутке
, то график является выпуклым вверх на промежутке 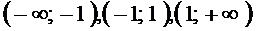 .
.
Точка  может быть точкой перегиба только в том случае, когда
может быть точкой перегиба только в том случае, когда 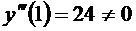 , либо
, либо  не существует – необходимое условие перегиба. Однако, равенство нулю или не существование второй производной в точке
не существует – необходимое условие перегиба. Однако, равенство нулю или не существование второй производной в точке  не означает еще, что в точке
не означает еще, что в точке  будет перегиб графика. Поэтому нужно дополнительно исследовать такие точки.
будет перегиб графика. Поэтому нужно дополнительно исследовать такие точки.
I правило. Если  равна нулю или не существует и
равна нулю или не существует и  при переводе через точку
при переводе через точку  меняет знак, то
меняет знак, то  ‑ точка перегиба графика функции
‑ точка перегиба графика функции  .
.
II правило.
Если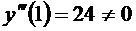 и
и 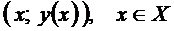 , то
, то 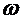 является точкой перегиба графика функции
является точкой перегиба графика функции 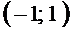 .
. Пример 4. Найти промежутки выпуклости и точки перегиба графика функции  .
.
Вычислим вторую производную  .
.
 ;
;
 .
.
Точки  и
и  разбивают числовую прямую на три промежутка:
разбивают числовую прямую на три промежутка:  . На промежутках
. На промежутках  вторая производная положительна, на промежутке
вторая производная положительна, на промежутке  ‑ отрицательна. Следовательно, график функции является выпуклым вниз на
‑ отрицательна. Следовательно, график функции является выпуклым вниз на  и выпуклым вверх на
и выпуклым вверх на  .
.
В точках  вторая производная равна нулю. Вычислим
вторая производная равна нулю. Вычислим  :
:  . Поскольку
. Поскольку  и
и  , то в точке
, то в точке  и в точке
и в точке  график функции имеет перегиб. 2.7
график функции имеет перегиб. 2.7