3.3. Теоремы о среднем. Правило Лопиталя.
Приведем (без доказательств) несколько теорем, утверждения которых играют большую роль в аппарате дифференциального исчисления.
1. Теорема Ролля о корнях производной. Если функция f(x) непрерывна на отрезке [a, b], дифференцируема в интервале (а, b) и f(a) = f(b), то в интервале (а, b) найдется хотя бы одно значение х = x, при котором f `(x) = 0.
Если f(a) = f(b) = 0 (частный случай), то теорема Ролля означает, что между двумя корнями функции содержится хотя бы один корень ее производной. Геометрическое истолкование: если непрерывная на отрезке [a, b] кривая имеет в каждой точке касательную, не параллельную оси Оу, и равные ординаты в точках а и b, то найдется по крайней мере одна точка x (a < x < b) такая, в которой касательная к кривой параллельна оси Ох (tga = f `(x) = 0).2. Теорема Лагранжа (о конечных приращениях): Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема в интервале (a, b), то в этом интервале найдется хотя бы одно значение х =x, при котором выполяется равенство f(b) – f(a) = (b – a) f `(x).
Геометрический смысл: на дуге АВ непрерывной кривой у = f(x) имеющей в каждой точке касательную не параллельную оси Оу найдется хотя бы одна точка x (a < x < b) такая, в которой касательная параллельна хорде АВ.
3. Теорема Коши (об отношении приращений двух функций): Если функции f(x) и j(x) непрерывны на отрезке [a, b] и дифференцируемы в интервале (a, b), причем j`(x) ? 0, то в этом интервале найдется хотя бы одно значение х = x ( a < x < b) такое, что  . Теорема Коши позволяет доказать два важных для решения задач теории пределов утверждения, известных под названием правила Лопиталя.
. Теорема Коши позволяет доказать два важных для решения задач теории пределов утверждения, известных под названием правила Лопиталя.
Теорема 1. Пусть функции f(x) и j(x) на некотором отрезке [a, b] удовлетворяют условиям теоремы Коши и обращаются в нуль точке а т.е.
f(a) = j(a) = 0; тогда, если существует  , то существует и
, то существует и  ,
,
причем  .
.
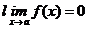 и
и 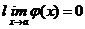 ; б) если f `(a) = j`(a) = 0, а функции f `(x) и j`(x) удовлетворяют условиям теоремы Коши, то, применяя правило Лопиталя дважды, получим
; б) если f `(a) = j`(a) = 0, а функции f `(x) и j`(x) удовлетворяют условиям теоремы Коши, то, применяя правило Лопиталя дважды, получим 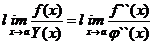 ; в) процедура (при выполнении соответствующих условий) может быть повторяема до получения результата.
; в) процедура (при выполнении соответствующих условий) может быть повторяема до получения результата. Правило справедливо и в случае  и
и  .
.
Теорема 2. Пусть функции f(x) и j(x) удовлетворяют условиям теоремы Коши при всех х ? а в окресности точки а,  и
и  , и пусть существует предел
, и пусть существует предел  . Тогда существует и предел
. Тогда существует и предел  , причем
, причем
 (3.28).
(3.28).
Это правило позволяет раскрывать неопределенности вида  . Оно справедливо и в случаях: а) А = ¥; б) х ® ¥.
. Оно справедливо и в случаях: а) А = ¥; б) х ® ¥.
Во многих случаях это правило позволяет раскрыть неопределенности и других видов, применив предварительно те или иные преобразования. Так, неопределенности вида 0 ? ¥ или ¥ – ¥ приводят к виду  или
или  путем алгебраических преобразований данной функции; в случае неопределенности вида 00, ¥0, или 1¥ следует прологарифмировать данную функцию и найти предел ее логарифма.
путем алгебраических преобразований данной функции; в случае неопределенности вида 00, ¥0, или 1¥ следует прологарифмировать данную функцию и найти предел ее логарифма.
Примеры:
1. Неопределенность вида (∞-∞) : (неопределенность вида
(неопределенность вида  , применяем правило Лопиталя). =
, применяем правило Лопиталя). =  (
( ;правило Лопиталя) =
;правило Лопиталя) = 
2. Неопределенность вида 00: . Обозначим
. Обозначим  . Прологарифмируем обе части равенства
. Прологарифмируем обе части равенства  (неопределенность вида ∞·0) =
(неопределенность вида ∞·0) =  (
(  ; правило Лопиталя) = class="lazyload" data-src="/files/uch_group46/uch_pgroup327/uch_uch1268/image/94.gif">(
; правило Лопиталя) = class="lazyload" data-src="/files/uch_group46/uch_pgroup327/uch_uch1268/image/94.gif">( ; правило Лопиталя) =
; правило Лопиталя) =  ;
;  ;
;  ℮0=1 т.е.
℮0=1 т.е.  ;
;