Тема №14. Статистическое моделирование

1) Разыгрывание дискретной случайной величины методом Монте–Карло

Сущность метода Монте–Карло состоит в следующем: требуется найти значение 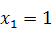некоторой изучаемой величины.

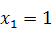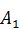Практически же поступают так: вычисляют (разыгрывают) возможных значений случайной величины X, находят их среднее арифметическое

и принимают в качестве оценки (приближенного значения) искомого числа :

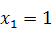Таким образом, для применения метода Монте–Карло необходимо уметь разыгрывать случайную величину.

Разыграть дискретную случайную величину X – это значит вычислить последовательность ее возможных значений (), зная закон распределения X.

Введем обозначения: R – непрерывная случайная величина, распределенная равномерно в интервале ; – случайные числа (возможные значения R).

Правило.

X
p

надо:

1) Разбить интервал оси на частичных интервалов:

2) Выбрать (например, из таблицы случайных чисел) случайное число .

Если попало в частичный интервал , то разыгрываемая величина приняла возможное значение .

2) Разыгрывание полной группы событий

Требуется разыграть испытания, в каждом из которых наступает одно из событий полной группы, вероятности которых известны. Разыгрывание полной группы событий сводится к разыгрыванию дискретной случайной величины.

Правило. Для того чтобы разыграть испытания, в каждом из которых наступает одно из событий полной группы, вероятности которых известны, достаточно разыграть (по правилу п 1)) дискретную случайную величину X со следующим

законом распределения:

X				class="lazyload" data-src="/files/uch_group46/uch_pgroup327/uch_uch1271/image/4013.gif">
p

Если в испытании величина X приняла возможное значение , то наступило событие .

3) Разыгрывание непрерывной случайной величины

Известна функция распределения непрерывной случайной величины X. Требуется разыграть X, т. е. вычислить последовательность возможных значений ().

1. Метод обратных функций.

Правило 1. Для того чтобы разыграть возможное значение непрерывной случайной величины X, зная ее функцию распределения , надо выбрать случайное число , приравнять его функции распределения и решить относительно полученное уравнение

Если известна плотность вероятности , то используют

Правило 2. Для того, чтобы разыграть возможное значение непрерывной случайной величины X, зная ее плотность вероятности , надо выбрать случайное число и решить относительно уравнение

или уравнение

где 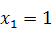– наименьшее конечное возможное значение Х.

2. Метод суперпозиции.

Правило 3. Для того чтобы разыграть возможное значение случайной величины I, функция распределения которой

где – функции распределения , , , надо выбрать два независимых случайных числа и и по случайному числу разыграть возможное значение вспомогательной дискретной случайной величины Z (по правилу 1):

Z
p

Если окажется, что , то решают относительно уравнение .

Замечание. Если задана плотность вероятности непрерывной случайной величины X в виде

где – плотности вероятностей, коэффициенты положительны, их сумма равна единице и если окажется, что , то решают (по правилу 2) относительно уравнение

или уравнение

4) Приближенное разыгрывание нормальной случайной величины

Требуется приближенно разыграть нормальную случайную величину.

Правило. Для того чтобы приближенно разыграть возможное значение нормальной случайной величины X с параметрами и , надо сложить 12 независимых случайных чисел и из полученной суммы вычесть 6:

Замечание. Если требуется приближенно разыграть нормальную случайную величину Z с математическим ожиданием 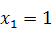и средним квадратическим отклонением , то, разыграв возможное значение по приведенному выше правилу, находят искомое возможное значение по формуле

5) Разыгрывание двумерной случайной величины

1. Дискретная двумерная случайная величина.

Разыгрывание дискретной двумерной случайной величины (X, Y) сводится к разыгрыванию ее составляющих – одномерных дискретных случайных величин X и У.

Пусть задан закон распределения двумерной случайной величины (X, Y). Если составляющие X и Y независимы, то находят законы их распределения и по ним разыгрывают X и Y по правилу п.1.

Если составляющие зависимы, то находят закон распределения одной из них, условные законы распределения другой и по ним разыгрывают X и Y по правилу п.1.

2. Непрерывная двумерная случайная величина.

Разыгрывание непрерывной двумерной случайной величины (X, Y) сводится к разыгрыванию ее составляющих – одномерных случайных величии X и Y.

Пусть задан закон распределения двумерной случайной величины (X, Y). Если составляющие X и Y независимы, то находят законы их распределения и по ним разыгрывают X и Y по правилам п.3.

Если составляющие X и Y зависимы, то находят закон распределения одной из них, условный закон распределения другой и по ним разыгрывают X и Y по правилам п.3.

Замечание. Составляющие X и Y независимы, если выполняется любое из условий:

1. Плотность совместного распределения равна произведению плотностей составляющих.

2. Функция совместного распределения равна произведению функций распределения составляющих.

3. Условные плотности распределения составляющих равны их безусловным плотностям.

4. Плотность совместного распределения равна произведению двух функций, одна из которых зависит только от , а другая – только от .

Пример1. Разыграть 8 значений дискретной случайной величины X, закон распределения которой задан в виде таблицы:

Решение: Разобьем интервал (0,1) на числовой оси точками с координатами , на три частичных интервала: .

Выпишем из таблицы случайных чисел 8, например: 0,14; 0,39; 0,06; 0,86; 0,87; 0,17; 0,17; 0,77.

Случайное число принадлежит частичному интервалу , поэтому разыгрываемая дискретная случайная величина приняла возможное значение . Случайное число принадлежит частичному интервалу , поэтому разыгрываемая дискретная случайная величина приняла возможное значение . Случайное число принадлежит частичному интервалу , поэтому разыгрываемая дискретная случайная величина приняла возможное значение . Аналогично получаем остальные возможные значения.

Таким образом, разыгранные значения X таковы: 3, 11, 3, 24, 24, 3, 3, 24.

Пример2. Разыграть 6 испытаний, в каждом из которых событие А появляется с вероятностью .

Решение: Выпишем из таблицы случайных чисел 6, например: 0,34; 0,24; 0,23; 0,38; 0,64; 0,36. Считая, что при событие А появилось, а при наступило противоположное событие, получим искомую последовательность событий: , , , , , .

Пример3. Заданы вероятности четырех событий , образующих полную группу 0,19; 0,21; 0,34; 0,26. Разыграть 5 испытаний, в каждом из которых появляется одно из перечисленных событий.

Решение: Определим дискретную случайную величины X, значения которой 1, 2, 3, 4 соответствуют рассматриваемым событиям с соответствующими вероятностями:

X
p	0,19	0,21	0,34	0,26

Решение: Разобьем интервал (0,1) на числовой оси точками с координатами , , на четыре частичных интервала: .

Выпишем из таблицы случайных чисел 5 чисел, например: 0,10; 0,37; 0,08; 0,99; 0,12.

Случайное число принадлежит частичному интервалу , поэтому разыгрываемая дискретная случайная величина приняла возможное значение , т.е. наступило событие . Случайное число принадлежит частичному интервалу , поэтому разыгрываемая дискретная случайная величина приняла возможное значение и, значит, наступило событие . Аналогично находим остальные события.

Таким образом, искомая последовательность событий такова: .

Пример4. События и независимы и совместны. Разыграть 6 испытаний, в каждом из которых вероятность появления события равна 0,6, а вероятность появления события равна 0,2.

Решение: Возможны следующие исходы испытания:

, т.е. произошли одновременно оба события. Так как и независимы, то Далее, , т.е. событие произошло, а нет, Если Событие не произошло, а наступило: , . И, наконец, , т.е. оба события одновременно не произошли

Теперь задача свелась к разыгрыванию полной группы событий: с вероятностью 0,12, с вероятностью 0,48, с вероятностью 0,08 и с вероятностью 0,32 (Пример3.)

В свою очередь, эта задача сводится к разыгрыванию дискретной случайной величины X (Пример1), закон распределения которой:

X
p	0,12	0,48	0,08	0,32

Решение: Разобьем интервал (0,1) на числовой оси точками с координатами , , на четыре частичных интервала: .

Выпишем из таблицы случайных чисел 6 чисел, например: 0,51; 0,92; 0,43; 0,37; 0,29, 0, 65.

Случайное число принадлежит частичному интервалу , поэтому разыгрываемая дискретная случайная величина приняла возможное значение , т.е. наступило событие . Случайное число принадлежит частичному интервалу , поэтому разыгрываемая дискретная случайная величина приняла возможное значение и, значит, наступило событие . Аналогично находим остальные события.

Таким образом, искомая последовательность событий такова: .

Пример5. Разыграть 10 возможных значений непрерывной случайной величины X, распределенной по нормальному закону с параметрами и . При этом воспользоваться таблицей случайных чисел, начав с числа . По полученной выборке оценить выборочное среднее и исправленное выборочное среднее квадратическое отклонение. Сравнить полученные значения с заданными параметрами.

Решение: Будем выбирать 10 раз по 12 случайных чисел, начиная с , находить их сумму и вычитать из нее 6, а затем, выполнив расчет по формуле , найдем значения разыгрываемой случайной величины:

i
1	0,80	0,95	0,90	0,91	0,17	0,39	0,29	0,27	0,49	0,45	0,66	0,06	0,34	2,34
2	0,57	0,47	0,17	0,20	0,63	0,61	0,04	0,02	0,00	0,82	0,29	0,16	–2,02	–0,02
3	0,65	0,31	0,06	0,01	0,08	0,05	0,15	0,95	0,33	0,47	0,64	0,35	–1,95	0,05
4	0,08	0,03	0,36	0,06	0,85	0,26	0,97	0,76	0,02	0,88	0,67	0,67	–0,39	1,61
5	0,43	0,97	0,04	0,43	0,62	0,76	0,59	0,63	0,57	0,33	0,21	0,35	–0,07	1,93
6	0,98	0,95	0,11	0,68	0,77	0,12	0,17	0,17	0,68	0,33	0,73	0,79	0,48	2,48
7	0,64	0,57	0,53	0,34	0,07	0,27	0,68	0,50	0,36	0,69	0,73	0,61	–0,01	1,99
8	0,70	0,65	0,81	0,33	0,98	0,85	0,45	0,57	0,18	0,24	0,06	0,35	0,17	2,17
9	0,30	0,34	0,26	0,14	0,86	0,79	0,90	0,74	0,39	0,02	0,05	0,16	–1,05	0,95
10	0,56	0,92	0,68	0,66	0,57	0,48	0,18	0,73	0,05	0,38	0,52	0,47	0,2	2,2

Найдем оценки параметров случайной величины

, .

Итак, , . Оценки удовлетворительные: близко к двум (к а), мало отличается от единицы (от ).

[5, гл.21], [6, гл.15]. Тема №15. Однофакторный дисперсионный анализ

Дисперсионным анализом называется статистический метод анализа результатов испытаний, цель которого — оценить влияние одного или нескольких качественных факторов на рассматриваемую величину X.

Схема однофакторного дисперсионного анализа рассмотрена ниже на примере исследования влияния различных видов рекламы на прибыль предприятия.

Если разделить виды рекламы на несколько групп (уровней фактора) и через одинаковые интервалы времени измерять прибыль, то результаты можно представить в виде таблицы:

Номер измерения	Уровни фактора
			…
1			…
2			…
…	…	…	…	…
q			…
Групповая средняя			…

Число измерений на каждом уровне считаем одинаковым и равным q. В последней строке помещены групповые средние для каждого уровня фактора.

Общую среднюю можно получить как среднее арифметическое групповых средних:

На разброс прибыли относительно общей средней влияют как изменения уровня рассматриваемого фактора, так и случайные факторы. Для того чтобы учесть влияние данного фактора, общая выборочная дисперсия разбивается на две части, первая из которых называется факторной (), а вторая — остаточной ( ).

С целью учета этих составляющих вначале рассчитываются общая сумма квадратов отклонений вариант от общей средней

и факторная сумма квадратов отклонений групповых средних от общей средней, которая и характеризует влияние данного фактора,

Последнее выражение получено путем замены каждой варианты в выражении групповой средней для данного фактора.

Остаточная сумма квадратов отклонений получается как разность

Для определения общей выборочной дисперсии необходимо разделить на число измерений pq:

а для получения несмещенной общей выборочной дисперсии это выражение нужно умножить на pq/(pq –1):

где pq – 1 – число степеней свободы несмещенной общей выборочной дисперсии.

Соответственно, для несмещенной факторной выборочной дисперсии

где р –1 – число степеней свободы несмещенной факторной выборочной дисперсии.

Для несмещенной остаточной выборочной дисперсии число степеней свободы будет равно разности

и выражение дисперсии примет вид

С целью оценки влияния фактора на изменения рассматриваемого параметра рассчитывается величина

Так как отношение двух выборочных дисперсий и распределено по закону Фишера — Снедекора, то полученное значение сравнивают со значением функции распределения в критической точке , соответствующей выбранному уровню значимости . Если , то фактор оказывает существенное воздействие и его следует учитывать, в противном случае он оказывает незначительное влияние, которым можно пренебречь.

Для расчета и могут быть использованы также формулы

Пример. Изделие железнодорожного транспорта испытывается пять раз на каждом из четырех уровней продолжительности времени работы class="lazyload" data-src="/files/uch_group46/uch_pgroup327/uch_uch1271/image/4184.gif">.

Число отказов в каждом испытании на каждом уровне работы занесено в таблицу. Методами однофакторного дисперсионного анализа при уровне значимости исследовать влияние времени работы изделия на число появления отказов.

i
1	360	560	520	390
2	470	610	570	570
3	500	640	590	630
4	580	660	580	610
5	670	660	790	650
Групповая средняя	516	626	610	570

Решение: Находим общую среднюю

Для расчета составляем таблицу квадратов вариант:

i
1	129600	313600	270400	152100
2	220900	372100	324900	324900
3	250000	409600	348100	396900
4	336400	435600	336400	372100
5	448900	435600	624100	422500
	1385800	1966500	1903900	1668500

Вычисляем :

Находим :

Получаем :

Определяем факторную и остаточную дисперсии:

Находим :

Для уровня значимости , чисел степеней свободы и находим .

В связи с тем, что , нулевую гипотезу о влиянии времени работы изделия на число появления отказов отвергаем.