Тема 8. Кривые второго порядка.
Алгебраической кривой второго порядка в системе координат  называется кривая
называется кривая  , общее уравнение которой имеет вид:
, общее уравнение которой имеет вид:
 ,
,
где числа  - не равны нулю одновременно.
- не равны нулю одновременно.
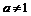 , то общее уравнение определяет кривую эллиптического типа (окружность (при
, то общее уравнение определяет кривую эллиптического типа (окружность (при 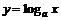 ), эллипс (при
), эллипс (при 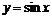 ), пустое множество, точку); 2) если
), пустое множество, точку); 2) если 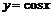 , то - кривую гиперболического типа (гиперболу, пару пересекающихся прямых); 3) если
, то - кривую гиперболического типа (гиперболу, пару пересекающихся прямых); 3) если 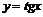 , то - кривую параболического типа (параболу, пустое множество, прямую, пару параллельных прямых) . Окружность, эллипс, гипербола и парабола называются невырожденными кривыми второго порядка.
, то - кривую параболического типа (параболу, пустое множество, прямую, пару параллельных прямых) . Окружность, эллипс, гипербола и парабола называются невырожденными кривыми второго порядка. Общее уравнение , где
, где  , определяющее невырожденную кривую (окружность, эллипс, гиперболу, параболу), всегда (методом выделения полных квадратов) можно привести к уравнению одного из следующих видов:
, определяющее невырожденную кривую (окружность, эллипс, гиперболу, параболу), всегда (методом выделения полных квадратов) можно привести к уравнению одного из следующих видов:
1а)  - уравнение окружности с центром в точке
- уравнение окружности с центром в точке  и радиусом
и радиусом  (рис.
(рис.
1б)  - уравнение эллипса с центром в точке
- уравнение эллипса с центром в точке  и осями симметрии, параллельными координатным осям. Числа
и осями симметрии, параллельными координатным осям. Числа  и
и  - называются полуосями эллипса; прямоугольник со сторонами
- называются полуосями эллипса; прямоугольник со сторонами  ,
,  параллельными осям симметрии и центром в точке
параллельными осям симметрии и центром в точке  - основным прямоугольником эллипса; точки пересечения основного прямоугольника с осями симметрии - вершинами эллипса.
- основным прямоугольником эллипса; точки пересечения основного прямоугольника с осями симметрии - вершинами эллипса.
Для построения эллипса в системе координат  :1) отмечаем центр
:1) отмечаем центр  эллипса; 2) проводим через центр пунктирной линией оси симметрии эллипса; 3) строим пунктиром основной прямоугольник эллипса с центром
эллипса; 2) проводим через центр пунктирной линией оси симметрии эллипса; 3) строим пунктиром основной прямоугольник эллипса с центром  и сторонами
и сторонами  ,
,  параллельными осям симметрии; 4) изображаем сплошной линией эллипс, вписывая его в основной прямоугольник так, чтобы эллипс касался его сторон только в вершинах эллипса (рис.8) .
параллельными осям симметрии; 4) изображаем сплошной линией эллипс, вписывая его в основной прямоугольник так, чтобы эллипс касался его сторон только в вершинах эллипса (рис.8) .
Аналогично строится и окружность, основной прямоугольник которой имеет стороны  (рис. 7).
(рис. 7).

Рис.7 Рис. 8
2)  - уравнения гипербол (называемых сопряжёнными) с центром в точке
- уравнения гипербол (называемых сопряжёнными) с центром в точке  и осями симметрии, параллельными координатным осям. Числа
и осями симметрии, параллельными координатным осям. Числа  и
и  - называются полуосями гипербол; прямоугольник со сторонами
- называются полуосями гипербол; прямоугольник со сторонами  ,
,  параллельными осям симметрии и центром в точке
параллельными осям симметрии и центром в точке  - основным прямоугольником гипербол; точки пересечения основного прямоугольника с осями симметрии - вершинами гипербол; прямые
- основным прямоугольником гипербол; точки пересечения основного прямоугольника с осями симметрии - вершинами гипербол; прямые  , проходящие через противоположные вершины основного прямоугольника – асимптотами гипербол.
, проходящие через противоположные вершины основного прямоугольника – асимптотами гипербол.
Для построения гиперболы в системе координат  : 1) отмечаем центр гиперболы
: 1) отмечаем центр гиперболы  ; 2) проводим через центр
; 2) проводим через центр  пунктирной линией оси симметрии гиперболы; 3) строим пунктиром основной прямоугольник гиперболы с центром
пунктирной линией оси симметрии гиперболы; 3) строим пунктиром основной прямоугольник гиперболы с центром  и сторонами
и сторонами  и
и  параллельными осям симметрии; 4) проводим через противоположные вершины основного прямоугольника пунктирной линией прямые, являющиеся асимптотами гиперболы, к которым неограниченно близко, при бесконечном удалении от начала координат, приближаются ветви гиперболы, не пересекая их; 5) изображаем сплошной линией ветви гиперболы
параллельными осям симметрии; 4) проводим через противоположные вершины основного прямоугольника пунктирной линией прямые, являющиеся асимптотами гиперболы, к которым неограниченно близко, при бесконечном удалении от начала координат, приближаются ветви гиперболы, не пересекая их; 5) изображаем сплошной линией ветви гиперболы  (рис. 9) или гиперболы
(рис. 9) или гиперболы  (рис. 10).
(рис. 10).

Рис.9 Рис. 10
3а)  - уравнение параболы с вершиной в точке
- уравнение параболы с вершиной в точке  и осью симметрии, параллельной координатной оси
и осью симметрии, параллельной координатной оси  (рис. 11).
(рис. 11).
3б)  - уравнение параболы с вершиной в точке
- уравнение параболы с вершиной в точке  и осью симметрии, параллельной координатной оси
и осью симметрии, параллельной координатной оси  (рис. 12).
(рис. 12).
Для построения параболы в системе координат  : 1) отмечаем вершину параболы
: 1) отмечаем вершину параболы  ; 2) проводим через вершину
; 2) проводим через вершину  пунктирной линией ось симметрии параболы; 3) изображаем сплошной линией параболу, направляя её ветвь, с учётом знака параметра параболы
пунктирной линией ось симметрии параболы; 3) изображаем сплошной линией параболу, направляя её ветвь, с учётом знака параметра параболы  : при
: при  - в положительную сторону координатной оси, параллельной оси симметрии параболы (рис. 11а и 12а); при
- в положительную сторону координатной оси, параллельной оси симметрии параболы (рис. 11а и 12а); при  - в отрицательную сторону координатной оси (рис.11б и 12б) .
- в отрицательную сторону координатной оси (рис.11б и 12б) .

Рис. 11а Рис. 11б

Рис. 12а Рис. 12б