6. Свойства степенных рядов.
Теорема 1. Сумма степенного ряда с радиусом сходимости R непрерывна во всех точках его промежутка сходимости.
Св-во2: (О почленном интегрировании).Пусть задан степенной ряд 
и f(x) – его сумма, определенная на Дc .
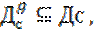х из области сходимости 
. 
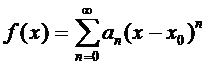(5).
Ряд (5) назыв-т проинтегрированным рядом по отношению к исходному.Он тоже явл степ-м рядом с радиусом сходимости Rn, д/ряда (5) справедливо. 
Св-во3:(о почленном дифференц-ии). Д/
степ ряд допускает почленное дифференцирование, причем 
(6). Полученный ряд (6) назыв дифференцированным по отношению к исходному и его область сходимости 
.
Следствие. Степенной ряд внутри промежутка сходимости допускает почленное дифференцирование любое количество раз.
7. Частичные суммы степенного ряда представляют собой многочлены поэтому хорошо вычисляются. Значит удобно при возможности представить ф-ию в виде суммы степенного ряда(//как говорят, разложить функцию ряд).
Пусть f(x) разложимый степенной ряд т.е. 
коэффи-ты а0,
,…, и x0: 
.
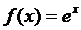с Дс то внутри этого промежутка степенной ряд можно бесконечно дифференцировать. Необходимое условие разложимости ф-ий в степен ряд явл бесконечн диффер-емость внутри её промежутка.
Рассм ф-ию f(x) в т. 
. Получим 
.f()=
. Продифференцируем ряд (*)
(**). Продифференцируем (**)
Продолжая процесс получаем, что 
- формула д/опред-я коэф-ов при разложении в степенной ряд. Т.о.ряд,в кот разлагается фу-ия, должен иметь вид:
- ряд Тейлора.
Д/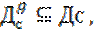 ф-ии бесконечно дифференцируемой в т.х0 ряд Тейлора 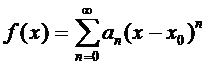. Сходимость ряда в этой точке надо исследовать.