Скалярное произведение векторов.
Определение. Скалярным произведением векторов 
и 
называется число, равное произведению длин этих сторон на косинус угла между ними.
? = ïïïïcosj
Свойства скалярного произведения:
1) ? = ïï2;
2) ?992" class="lazyload" data-src="/files/uch_group46/uch_pgroup327/uch_uch1271/image/155.gif"> = 0, если ^ или = 0 или = 0.
3) ? = ?;
4) ?(+
) = ?+ ?;
5) (m)? = ?(m) = m(?); m=const
Если рассматривать векторы 
в декартовой прямоугольной системе координат, то
? = xa xb + ya yb + za zb;
Используя полученные равенства, получаем формулу для вычисления угла между векторами:
;
Пример.
Найти (5 + 3)(2 – ), если 
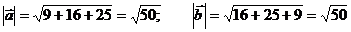
10?– 5?+ 6?– 3? = 10
,
т.к. 
.
Пример. Найти угол между векторами и , если 
.
Т.е. = (1, 2, 3), = (6, 4, –2)
?= 6 + 8 – 6 = 8:
.
cosj = 
Пример. Найти скалярное произведение (3 – 2)?(5 – 6), если 
15?– 18?– 10?+ 12? = 15
+ 12?36 = 240 – 336 + 432 = 672 – 336 = 336.
Пример. Найти угол между векторами и , если 
.
Т.е. = (3, 4, 5), = (4, 5, –3)
?= 12 + 20 – 15 =17 :
.
cosj = 
Пример. При каком m векторы 
и 
перпендикулярны.
= (m, 1, 0); = (3, –3, –4)
.
Пример. Найти скалярное произведение векторов 
и 
, если 
()() = 
= 10 +
+ 27 + 51 + 135 + 72 + 252 = 547.