Решение задач
Пример1 Вычислить по формуле прямоугольников определенный интеграл  . Оценить погрешность вычислений.
. Оценить погрешность вычислений.
Решение:
Положим n=10, т.е.
разбиваем интеграл интегрирования от 1 до 2 на десять равных частей.
Вычислим значение функции в точках разбиения:
X0=1 
X1=1,1 
X2=1,2 
X3=1,3 
X4=1,4 
X5=1,5 
X6=1,6 
X7=1,7 
X8=1,8 
X9=1,9 
Сумма 7,18773
По формуле (-) получаем:
 .
.
Полученное значение больше истинного, т.к. кривая  обращена к оси x своей выпуклостью.
обращена к оси x своей выпуклостью.
Вычислим остаточный член по формуле (-). Для этого предварительно определяем первую производную подынтегральной функции:

представляет собой убывающую функцию и следовательно максимальное значение принимает при меньшем x из заданного интервала  , т.е.
, т.е.
 .
.
Подставляя в формулу (-), окончательно получаем:
 .
.
Ошибка округления существенно меньше полученного R и, следовательно, её можно не учитывать.
Окончательно получаем:
 .
.
Вычисление по методу прямоугольников значение определенного интеграла оказалось достаточно грубым. Для получения более точного результата следует уменьшить шаг разбиения.
Пример2 Вычислить по формуле трапеций определенный интеграл  . Определить погрешность вычислений.
. Определить погрешность вычислений.
Решение:
Положим n=10. воспользуемся вычисленным в примере 1 значениями функциями в точках разбиения. По формуле (-) найдем значение определенного интеграла:
 =0,1*(
=0,1*( *1*0,90909+0,83333+0,76923+0,71429+0,66667+
*1*0,90909+0,83333+0,76923+0,71429+0,66667+
+0,625+0,55556+0,58824+0,52632+ )=0,69377.
)=0,69377.
Оценим погрешность вычислений. Полная погрешность R0 складывается из погрешности арифметических действий  и остаточного члена R.
и остаточного члена R.
 ,
,
где  -коэффициенты формулы трапеции и
-коэффициенты формулы трапеции и  - максимальная ошибка округления значений подынтегральной функции.
- максимальная ошибка округления значений подынтегральной функции.
 .
.
Остаточный член оценим по формуле (-), предварительно определив максимальное значение второй производной функции на заданном интервале интегрирования.
 ;
;
 .
.
 - убывающая функция, на интервале
- убывающая функция, на интервале  наибольшее значение имеет в точке x =1.
наибольшее значение имеет в точке x =1.
 .
.
По формуле (-) получаем:
 .
.
 существенно меньше R, поэтому можно считать
существенно меньше R, поэтому можно считать  .
.
С учетом точного решения заданного определенного интеграла, абсолютная погрешность численного интегрирования методом трапеций:
0,69377-0,69315=0,00062class="lazyload" data-src="/files/uch_group46/uch_pgroup327/uch_uch1421/image/589.gif">
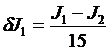
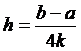
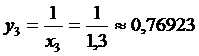
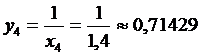
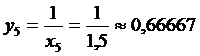
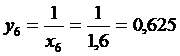
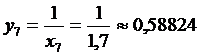
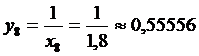
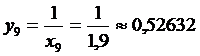
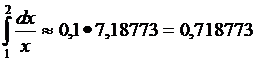
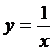
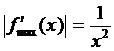
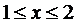
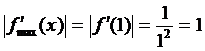
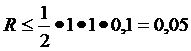
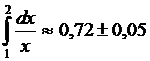
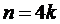
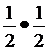
Пример 5 Составить горизонтальную таблицу разностей функции 
Начальное значение принять равным нулю:  , шаг равным единице:
, шаг равным единице:  .
.
Решение:
Вычислим значения функции в некоторых узловых точках. При:
X0=0 y0=03-02+6·0-4=-4
X1=1 y1=13-12+6∙1-4=2
X2=2 y2=23-22+6·2-4=12
X3=3 y3=33-32+6∙3-4=32
X4=4 y4=43-42+6·4-4=68
X5=5 y5=53-52+6·5-4=126
…….. ………………………….
По формулам вычислим конечные разности различных порядков и занесем их в таблицу



Данная функция  является полиномом третьей степени, поэтому третья разность постоянна и вычисляется по формуле (-):
является полиномом третьей степени, поэтому третья разность постоянна и вычисляется по формуле (-):
 .
.
Дальнейшее заполнение таблицы удобно производить при помощи суммирования уже вычисленных значений величин.
Согласно формулам (3.19): 
Отсюда: 


Таким образом, столбец 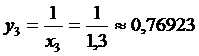 получается добавлением значения третьей разности (числа 6) к каждому вышестоящему элементу.
получается добавлением значения третьей разности (числа 6) к каждому вышестоящему элементу.
Для формирования столбца 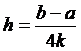 из получаем формулу:
из получаем формулу: 

Каждый элемент столбца 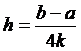 представляет собой сумму вышестоящего числа в этом столбце и соседнего с ним в столбце
представляет собой сумму вышестоящего числа в этом столбце и соседнего с ним в столбце 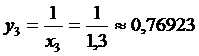 . (См. стрелку в таблице.)
. (См. стрелку в таблице.)
Используя формулы, для элементов столбца y получаем выражение, существенно облегчающее вычисление значений функции в узловых точках:


Правило заполнения столбца y такое же, как у столбца 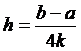 .
.
Ступенчатой ломанной отмечены исходные данные, необходимые для заполнения таблицы по указанным правилам.
| x | y | 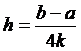 | 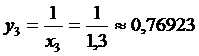 | 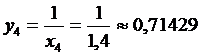 |
| 0 | -4 | 6 | 4 | 6 |
| 1 | 2 | 10 |   10 10 | +6 |
| 2 | 12 |   20 20 | +16 | 6 |
| 3 |  32 32 | +36 | 22 | 6 |
| 4 | 68 | 58 | 28 | 6 |
| 5 |  126 126 | 86 | 34 | 6 |
| 6 | 212 | 120 | 40 | 6 |
| … | … | … | … | … |
Пример 6 Найти производную функции , заданной таблично в точке
, заданной таблично в точке  .
.
| x | y |
| 30 | 1,4771 |
| 35 | 1,5441 |
| 40 | 1,6021 |
| 45 | 1,6532 |
| 50 | 1,6990 |
Значения функции .
.
Решение:
Здесь шаг  .
.










Заполним таблицу разностей:
| i | x | y | 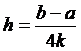 | 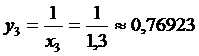 | 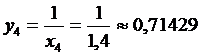 |  |
| 0 | 30 | 1,4771 | 0.0670 | -0,0090 | 0,0021 | -0,0005 |
| 1 | 35 | 1,5441 | 0,0580 | -0,0069 | 0,0016 | |
| 2 | 40 | 1,6021 | 0,0511 | -0,0053 | ||
| 3 | 45 | 1,6532 | 0,0458 | |||
| 4 | 50 | 1,6990 |
Отметим, что на практике таблицу конечных разностей заполняют сразу по правилам разобранных в примере -. Вычисление разностей по формулам (-) мы привели в качестве проверки.
По формуле (-), используя первую строчку таблицы, с точностью до разностей четвертого порядка, получаем:

 .
.
Оценим точность найденного значения. Заданная таблично функция есть  . Производная этой функции:
. Производная этой функции:
 .
.
При  получим:
получим:
 .
.
Таким образом, результаты совпали с точностью до четвертого десятичного знака.
Пример 7
По табличным данным найти аналитическое выражение производной.
 | 0 | 1 | 2 | 3 | 4 | 5 |
 | 10,4 | 16 | 20,8 | 24,8 | 28 | 30,4 |
Решение:
Составим таблицу конечных разностей, обозначив  :
:
 |  |  |  |  |  |
| 0 | 0 | 10,4 | 5,6 | -0,8 | 0 |
| 1 | 1 | 16 | 4,8 | -0,8 | 0 |
| 2 | 2 | 20,8 | 4 | -0,8 | 0 |
| 3 | 3 | 24,8 | 3,2 | -0,8 | |
| 4 | 4 | 28 | 2,4 | ||
| 5 | 5 | 30,4 |
Воспользуемся интерполяционной формулой Ньютона в форме (-):

Слагаемое, содержащее третью конечную разность не записываем, т.к.  .
.
Учтем, что  .
.
По таблице определяем:  .
.
Следовательно, .
.
 ,
,
 ,
,
 .
.