2.2. Предел. Непрерывность функции.
Переменную величину х называют упорядоченной, если известна область D изменения ее и про каждое из двух любых значений можно сказать, какое предыдущее и какое последующее.
 Рассмотрим упорядоченную переменную, изменяющуюся специальным образом, определяемым термином «Переменная величина стремится к пределу».
Рассмотрим упорядоченную переменную, изменяющуюся специальным образом, определяемым термином «Переменная величина стремится к пределу».
Число а называют пределом переменной х, если для всякого сколь угодно малого положительного e можно указать такое значение х, начиная с которого все последующие значения будут удовлетворять неравенству |x –а|bgcolor=white>
| Рис. 2.1. |

|
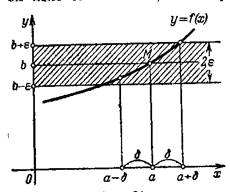 . Геометрическая интерпретация (рис.2.2.) – для всех точек х отстоящих от а не более чем на d, точки М графика функции у = f(x) лежат внутри полосы шириной 2e, ограниченной прямыми у = b –e и y = b + e.
. Геометрическая интерпретация (рис.2.2.) – для всех точек х отстоящих от а не более чем на d, точки М графика функции у = f(x) лежат внутри полосы шириной 2e, ограниченной прямыми у = b –e и y = b + e. Если х < а и х ® а, то пишут х ® а – 0; если х > а и х ® а – пишут х ® а + 0. Числа  и
и  называют левым и правым пределом функции f(x) в точке а.
называют левым и правым пределом функции f(x) в точке а.
Говорят, что функция f(x) стремится к пределу b при х ® ¥, если для всякого e > 0 можно указать такое N > 0, что для всех х удовлетворяющих условию |x| > N будет выполняться неравенство |f(x) – b| < e.
Функция f(x) стремится к бесконечности при х ® а, (является бесконечно большой при х ® а) если для всякого M > 0, как бы велико оно ни было, можно найти такое d > 0, что для всех х ? а и удовлетворяющих условию |x – a| < d имеет место |f(x)| > M, т.е.  (При этом возможно как
(При этом возможно как  , так и
, так и  ). Отметим, что функция может и не стремиться к конечному пределу при х ® а или х ® ¥. Примеры: у = sin x не имеет предела при х ® ¥, а у = sin 1/x – при х ® 0.
). Отметим, что функция может и не стремиться к конечному пределу при х ® а или х ® ¥. Примеры: у = sin x не имеет предела при х ® ¥, а у = sin 1/x – при х ® 0.
Функция a(х) называется бесконечно малой при х ® а или х ® ¥, если  или
или  .
.
Говорят, что если a(х) и b(х) – бесконечно малые при х ® а, и:
1)  (или
(или  ) – то a – бесконечно малая высшего порядка по сравнению с b и пишут a = 0 (b).
) – то a – бесконечно малая высшего порядка по сравнению с b и пишут a = 0 (b).
2)  , где m – число отличное от нуля, то a и b бесконечно малые одного порядка. Если m = 1, a и b – эквивалентные бесконечно малые, что можно записать используя уже знакомый символ эквивалентности: a ~b.
, где m – число отличное от нуля, то a и b бесконечно малые одного порядка. Если m = 1, a и b – эквивалентные бесконечно малые, что можно записать используя уже знакомый символ эквивалентности: a ~b.
3)  , где m - число отличное от нуля, то a- бесконечно малая n-го порядка по сравнению с b (т.е.
, где m - число отличное от нуля, то a- бесконечно малая n-го порядка по сравнению с b (т.е.
Отметим, что предел отношения бесконечно малых не изменится при замене их (или одной из них) эквивалентными бесконечно малыми. Это позволяет упростить решение многих задач теории пределов.
Аналогично сравниваются и бесконечно большие функции.
Связь между бесконечно малыми и бесконечно большими функциями определяется теоремой: если a(х) - бесконечно малая при х ® а, то функция f(x)=1/a(x) - бесконечно большая при х ® а, и обратно, если f(x) - бесконено большая при x ® а, то a(x)=1/f(x) - бесконечно малая при х ® а
Основные теоремы о пределах.
1. Предел алгебраической суммы двух, трех и вообще определенного числа переменных равен алгебраической сумме пределов этих переменных, т.е.
lim (u1 + u2 + … + un) = lim u1+ lim u2+ … + lim un
2. Предел произведения определенного числа переменнных равен произведению пределов этих переменных, т.е.
lim (u1 ? u2 ? … ? un) = lim u1 ? lim u2 ? … ? lim un
3. Предел частного двух переменных равен частному пределов этих переменных, если предел знаменателя отличен от нуля, т.е.  если lim V ? 0.
если lim V ? 0.
3. Если для соответствующих значений функций u = u(x), z = z(x), v = v(x) выполняются неравенства u £ z £ v и при этом u(x) и v(x) при х ® а (или х ® ¥) стремятся к одному и тому же пределу b, то z = z(x) при х ® а (или х ® ¥) стремится к тому же пределу.
Теорема 4 позволяет доказать справедливость важного соотношения, называемого первым замечательным пределом.  (2.1)
(2.1)
Из (2.1) следует эквивалентность бесконечно малых х и sin x: sin x ~x.
 Удобно пояснить это графически. На рис. 2.3 приведены графики функций у = х и у = sinх. Легко видеть, что чем меньше х отличается от нуля, тем меньше отличие ординат (значений функций) соответствующих графиков, а при х = 0 они совпадают.
Удобно пояснить это графически. На рис. 2.3 приведены графики функций у = х и у = sinх. Легко видеть, что чем меньше х отличается от нуля, тем меньше отличие ординат (значений функций) соответствующих графиков, а при х = 0 они совпадают.
Еще одно важное соотношение теории пределов, называемое вторым замечательным пределом имеет вид:  (2.2)
(2.2)
Число е – иррациональное (также как и число p) и может быть записано в виде бесконечной десятичной непериодической дроби е = 2,71828…; играет важную роль в вычислительной математике, служа, в частности, основанием натурального логарифма, обозначаемого ln x = logex. Функцию у = ех называют экспоненциальной функцией (иногда обозначается как ехр х ). В решении задач теории пределов могут быть полезны следующие равенства: 

 . Можно также заменять бесконечно малые величины эквивалентными им:
. Можно также заменять бесконечно малые величины эквивалентными им:

Непрерывность функций. Функцию у = f(х) называют непрерывной в точке а если:
1.Эта функция определена в некоторой окрестности точки а и в самой точке;
2.Существует предел функции  и он равен значению функции в этой точке, т.е.
и он равен значению функции в этой точке, т.е.  . Можно предложить и иное определение. Пусть аргумент х0 получит приращение Dх и примет значение х = х0 + Dх. В общем случае функция также получит некоторое приращение Dу = f(х0 + Dх) – f(х0).
. Можно предложить и иное определение. Пусть аргумент х0 получит приращение Dх и примет значение х = х0 + Dх. В общем случае функция также получит некоторое приращение Dу = f(х0 + Dх) – f(х0).
Функцию f(х) называют непрерывной в точке х0, если она определена в этой точке и некоторой окрестности ее и если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т.е.
 (2.3) или
(2.3) или  (2.3`)
(2.3`)
Приведем формулировку теоремы: Всякая элементарная функция непрерывна в каждой точке, в которой она определена и получим важное для решения задач теории пределов следствие.
Запишем условие непрерывности в виде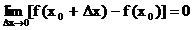 или, что тоже самое,
или, что тоже самое, 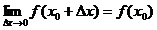 . Но
. Но 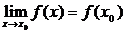 и, следовательно,
и, следовательно, 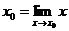 (2.4), т.е. для любой непрерывной функции во всех точках области определения ее справедливо соотношение (2.4) – предел функции равен функции предела (символы (и соответствующие операции) предела и функции можно поменять местами):
(2.4), т.е. для любой непрерывной функции во всех точках области определения ее справедливо соотношение (2.4) – предел функции равен функции предела (символы (и соответствующие операции) предела и функции можно поменять местами): 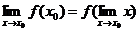 .
. Пример: 
В ряде случаев удобно использовать следующее соотношение:
 .
.
Говорят, что если функция f(x) непрерывна в каждой точке некоторого интервала (а, b), где a < b, то функция непрерывна на этом интервале. Точка внутри или на границе области определения, в которой нарушается условие непрерывности, называется точкой разрыва. Если существуют конечные пределы  и
и  , причем не все три числа b1, b2 и f(a) равны между собой, точка а называется точкой разрыва первого рода. Эти точки подразделяются на точки скачка, когда b1 ? b2 (скачок равен b2 - b1) и точки устранимого разрыва, когда b1 = b2. Точки разрыва , не являющиеся точками разрыва первого рода, называются точками разрыва второго рода. В этих точках не существует хотя бы один из односторонних пределов (Пример – “бесконечный” разрыв:
, причем не все три числа b1, b2 и f(a) равны между собой, точка а называется точкой разрыва первого рода. Эти точки подразделяются на точки скачка, когда b1 ? b2 (скачок равен b2 - b1) и точки устранимого разрыва, когда b1 = b2. Точки разрыва , не являющиеся точками разрыва первого рода, называются точками разрыва второго рода. В этих точках не существует хотя бы один из односторонних пределов (Пример – “бесконечный” разрыв:  ).
).
Рассмотрим некоторые свойства непрерывных функций (доказательства теорем можно найти в рекомендуемой литературе).
1. Если функция f(x) непрерывна на некотором отрезке [a, b], то на этом отрезке найдется по крайней мере одна точка х = х1 такая, что значение функции в этой точке будет удовлетворять соотношению f(x1) ? f(x), где х – любая другая точка отрезка, и найдется по крайней мере одна точка х2 такая, что значение функции в этой точке будет удовлетворять соотношению f(x2) ≤ f(x).
|
 f(x) на этом отрезке. Поясним с помощью рис. 2.4, на котором представлены графики трех непрерывных на [a, b] функций у1, у2 и у3. Легко видеть, что на интервале [a, b] функция у1 один раз достигает наибольшего М и наименьшего m значений. Функция у2 во всех точках [a, b] имеет одно и то же значение – оно одновременно и наибольшее и наименьшее. Функция у3 на [a, b] дважды принимает наибольшее М и наименьшее m значения. Но хоть один раз наибольшее и наименьшее значения принимает каждая из них!
f(x) на этом отрезке. Поясним с помощью рис. 2.4, на котором представлены графики трех непрерывных на [a, b] функций у1, у2 и у3. Легко видеть, что на интервале [a, b] функция у1 один раз достигает наибольшего М и наименьшего m значений. Функция у2 во всех точках [a, b] имеет одно и то же значение – оно одновременно и наибольшее и наименьшее. Функция у3 на [a, b] дважды принимает наибольшее М и наименьшее m значения. Но хоть один раз наибольшее и наименьшее значения принимает каждая из них!
(Отметим, что на интервале (а, b) утверждение теоремы может оказаться неверным. Пример: у = х – функция не имеет на интервале (а, b) наибольшего и наименьшего значений, т.к. не достигает значений а и b !)

|
3. Если функция f(x) определена и непрерывна на отрезке [a, b] и на концах этого отрезка принимает неравные значения f(a) = A и f(b) = B то, каково бы ни было число m, заключенное между числами А и В, найдется такая точка х = с, заключенная между a и b, что f(c) = m (легко видеть, что теорема 2 является частным случаем теоремы 3).
Следствие: Если функция f(x) непрерывна на некотором интервале и принимает на нем наибольшее и наименьшее значения, то на этом интервале она принимает по крайней мере один раз любое значение, заключенное между ее наибольшим и наименьшим значениями.
Контрольные вопросы.
1) Что называется пределом переменной, пределом функции?
2) Что называется бесконечно малой функцией?
3) Поясните графически первый замечательный предел?
4) Какая функция называется непрерывной в точке?
5) Какая точка называется точкой разрыва I рода, II рода (в чём отличие)?
6) Что является наибольшим и наименьшим значением функции на отрезке?
Тест 15.
1) Найти предел функции  при х, стремящемся к нулю справа?
при х, стремящемся к нулю справа?
а) 0;
б)  ;
;
в)  ;
;
г) не существует.
2) Пользуясь основными теоремами о пределах найти:  :
:
а) –2;
б) 0;
в)  ;
;
г)  .
.