Положительные ряды
Среди числовых рядов выделяются ряды, все члены которых неотрицательны. Такие ряды называют положительными. У такого ряда последовательность  его частных сумм является возрастающей и, поэтому, доя его сходимости достаточно, чтобы последовательность
его частных сумм является возрастающей и, поэтому, доя его сходимости достаточно, чтобы последовательность  была ограниченной.
была ограниченной.
Будем рассматривать два положительных ряда
 | (4) |
 | (5) |
1°. Пусть существует номер  такой, что
такой, что  .
.
Если ряд (5) сходится, то сходится и ряд (4). Если ряд (4) расходится, то расходится и ряд (5).
Пример 4. Рассмотрим ряд  . Сравним этот ряд с гармоническим рядом
. Сравним этот ряд с гармоническим рядом  . Так как
. Так как  , то ряд
, то ряд  расходится.
расходится.
Пример 5. Рассмотрим ряд  . Сравним его со сходящимся геометрическим рядом
. Сравним его со сходящимся геометрическим рядом  . Поскольку
. Поскольку  , то ряд
, то ряд  сходится.
сходится.
2°. Пусть существует конечный или бесконечный предел  .
.
a). Если  , то из сходимости ряда (5) следует сходимость ряда (4).
, то из сходимости ряда (5) следует сходимость ряда (4).
b). Если  , то из расходимости ряда (5) следует расходимость ряда (4).
, то из расходимости ряда (5) следует расходимость ряда (4).
Пример 6. Рассмотрим ряд  . Сравним его с гармоническим рядом. Поскольку
. Сравним его с гармоническим рядом. Поскольку  при
при 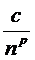 , то ряд
, то ряд  расходится.
расходится.
Пример 7. Рассмотрим ряд  . Сравним его со сходящимся геометрическим рядом
. Сравним его со сходящимся геометрическим рядом  . Так как
. Так как  при
при 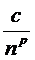 , то ряд
, то ряд  сходится.
сходится.
Для положительных рядов доказаны признаки, позволяющие сделать вывод о сходимости или расходимости ряда, изучая поведение при 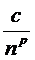 его
его  -го члена.
-го члена.
Признак Даламбера. Пусть существует предел  .
.
Если  , то ряд
, то ряд  сходится.
сходится.
Если class="lazyload" data-src="/files/uch_group46/uch_pgroup327/uch_uch1514/image/564.gif">, то ряд  расходится.
расходится.
Пример 8.
Рассмотрим ряд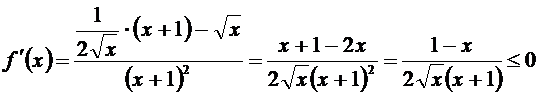 . Для этого ряда
. Для этого ряда 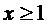 при
при 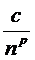 . По признаку Даламбера ряд сходится.
. По признаку Даламбера ряд сходится. Пример 9. Рассмотрим ряд  . Для этого ряда
. Для этого ряда  при
при 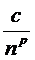 . По признаку Даламбера ряд расходится.
. По признаку Даламбера ряд расходится.
Признак Коши. Пусть существует предел  .
.
Если  , то ряд
, то ряд  сходится.
сходится.
Если  , то ряд
, то ряд  расходится.
расходится.
Пример 10. Рассмотрим ряд  . Для этого ряда
. Для этого ряда  По признаку Коши ряд сходится.
По признаку Коши ряд сходится.
Пример 11. Рассмотрим ряд  . Для этого ряда
. Для этого ряда  . Значит, ряд расходится.
. Значит, ряд расходится.
Заметим, то признаки Даламбера и Коши не дают ответа, когда  или
или  . В этом случае можно исследовать ряд с помощью других признаков.
. В этом случае можно исследовать ряд с помощью других признаков.
Интегральный признак. Пусть  ‑ положительная неубывающая функция, такая что
‑ положительная неубывающая функция, такая что  . Если последовательность
. Если последовательность 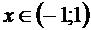 ,
,  сходится, то сходится и ряд
сходится, то сходится и ряд  .
.
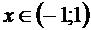 расходится, то расходится и исходный ряд.
расходится, то расходится и исходный ряд. Пример 12. Рассмотрим ряд  (этот ряд называют обобщенным гармоническим рядом).
(этот ряд называют обобщенным гармоническим рядом).
Функция  убывающая, положительная и
убывающая, положительная и  ,
,  ,
,  .
.
Если  , то
, то  . Так как
. Так как  при
при 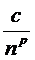 , то последовательность
, то последовательность 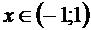 расходится, значит, расходится и ряд. Впрочем, при
расходится, значит, расходится и ряд. Впрочем, при  исследуемый ряд – гармонический, и его расходимость была доказана ранее.
исследуемый ряд – гармонический, и его расходимость была доказана ранее.
Если  , то
, то  .
.
При  ,
,  ; при
; при 
 . Таким образом, последовательность
. Таким образом, последовательность 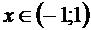 сходится при
сходится при  и расходится при
и расходится при  .
.
Вывод. Обобщенный гармонический ряд сходится при  и расходится при
и расходится при  .
.
Пример 13. Рассмотрим ряд  .
.
Функция  ;
;
 при
при 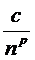 .
.
Значит, ряд расходится.
Если в признаке сравнения 2° в качестве эталонного использовать обобщенный гармонический ряд, то можно получить так называемый степенной признак сходимости положительных рядов. Этот признак дает ответ на вопрос о сходимости ряда в некоторых случаях, когда признаки Коши и Даламбера ответа не дают.
Степенной признак. Пусть  при
при 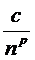 , где
, где  . Тогда при
. Тогда при  ряд расходится. При
ряд расходится. При  ряд сходится (условие
ряд сходится (условие  равносильно тому, что
равносильно тому, что  при
при 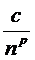 . Говорят, что
. Говорят, что  эквивалентен
эквивалентен  при
при 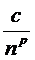 ).
).
Пример 14. Рассмотрим ряд  . Для этого ряда
. Для этого ряда  , значит, признак Даламбера не дает ответа на вопрос о сходимости ряда. Можно убедиться, что и признак Коши не приведет к желаемому результату.
, значит, признак Даламбера не дает ответа на вопрос о сходимости ряда. Можно убедиться, что и признак Коши не приведет к желаемому результату.
В то же время,  эквивалентен
эквивалентен  , так как
, так как  при
при 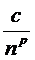 . Значит, в этом случае
. Значит, в этом случае  и, следовательно, ряд сходится по степенному признаку.
и, следовательно, ряд сходится по степенному признаку.
Пример 15. Ряд  имеет
имеет  -й член
-й член  , который эквивалентен
, который эквивалентен  . Значит, ряд расходится.
. Значит, ряд расходится.