Основные понятия
Пусть 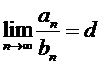 ‑ последовательность действительных чисел. Рассмотрим последовательность
‑ последовательность действительных чисел. Рассмотрим последовательность 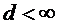 , построенную следующим образом:
, построенную следующим образом:
 ;
;
 ;
;
 ;
;

 ;
;

Последовательность 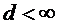 удобно записывать в виде
удобно записывать в виде  .
.
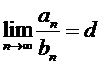 называют членами или элементами ряда. Числовой ряд задают обычно перечислением его элементов или указанием формулы, с помощью которой для заданного
называют членами или элементами ряда. Числовой ряд задают обычно перечислением его элементов или указанием формулы, с помощью которой для заданного  можно вычислить
можно вычислить  -й член ряда.
-й член ряда. Пример 1. Ряд  имеет
имеет  -й член
-й член  .
.
Поэтому 
т.е.  .
.
Рассмотрим ряд
 | (1) |
Сумму  называют
называют  -й частной суммой ряда (1).
-й частной суммой ряда (1).
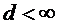 частных сумм ряда (1) сходится, то ряд (1) называют сходящимся, а число
частных сумм ряда (1) сходится, то ряд (1) называют сходящимся, а число 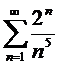 называют суммой ряда. Если же последовательность
называют суммой ряда. Если же последовательность 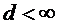 не имеет конечного предела, то ряд (1) называют расходящимся.
не имеет конечного предела, то ряд (1) называют расходящимся. Пример 2. Рассмотрим ряд  . Для него
. Для него  , что представляет собой сумму первых
, что представляет собой сумму первых 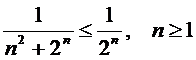 членов геометрической прогрессии.
членов геометрической прогрессии.
Если  , то
, то  и
и  .
.
Если  , то
, то  и
и  .
.
Если  , то
, то  и
и  .
.
Если  , то
, то 
и  не существует.
не существует.
Таким образом, ряд  при
при  сходится и расходится при
сходится и расходится при  . Этот ряд называется геометрическим.
. Этот ряд называется геометрическим.
Пусть ряд (1) сходится и  ‑ его сумма.
‑ его сумма.
 , , | (2) |
то при  получаем
получаем  .
.
Откуда следует необходимое условие сходимости ряда: если ряд сходится, то
 . . | (3) |
Если условие (3) не выполнено. То ряд расходится.
Пример 3. Ряд  расходится, т.к.
расходится, т.к.  и
и  .
.
Условие (3) не является достаточным для сходимости рядя. Даже если оно выполнено, ряд может расходится. Покажем это на примере гармонического ряда  . Для этого ряда
. Для этого ряда  при
при  , т.е. условие (3) выполнено. В то же время,
, т.е. условие (3) выполнено. В то же время,
 ,
,
 .
.
Поэтому  .
.
Предположим, что гармонический ряд сходится и  ‑ его сумма, т.е.
‑ его сумма, т.е.  при
при  . Поскольку
. Поскольку  , то при
, то при  получаем
получаем  ‑ противоречие. Значит, предположение о сходимости гармонического ряда было неверным.
‑ противоречие. Значит, предположение о сходимости гармонического ряда было неверным.
Несколько первых членов ряда не влияют на его сходимость. Если у ряда (1) удалить несколько первых членов, то получим ряд  , называемый остатком ряда (1). Сходимость ряда равносильна сходимости его любого остатка. 6.2
, называемый остатком ряда (1). Сходимость ряда равносильна сходимости его любого остатка. 6.2