Основные понятия
Как следует из предыдущего раздела, интеграл ‑ важнейшее понятие математического анализа. Неопределенным интегралом функции  (обозначается
(обозначается  ) называется совокупность функций
) называется совокупность функций  , у которых производная в каждой точке равна
, у которых производная в каждой точке равна  .
.
 . Функции из этой совокупности отличаются на постоянную величину, так что можно записать
. Функции из этой совокупности отличаются на постоянную величину, так что можно записать  .
. Определенным интегралом функции 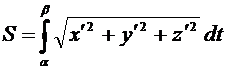 от
от  до
до  (обозначается
(обозначается  ) называется разность
) называется разность  , где
, где  ‑ любая из первообразных. Если функция
‑ любая из первообразных. Если функция 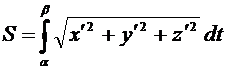 положительная и непрерывная, то
положительная и непрерывная, то  равен площади фигуры, ограниченной кривой
равен площади фигуры, ограниченной кривой  , осью абсцисс и прямыми
, осью абсцисс и прямыми  .
.
Определенный интеграл (если 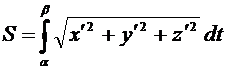 ‑ непрерывная функция) можно представить следующим образом. Разобьем отрезок
‑ непрерывная функция) можно представить следующим образом. Разобьем отрезок  на отрезки
на отрезки  ,
,  ,
,  ,
,  . Взяв на каждом отрезке произвольную точку
. Взяв на каждом отрезке произвольную точку  , составим сумму:
, составим сумму:
 .
.
Предел этой суммы при  стремящемся к нулю, равен
стремящемся к нулю, равен  . Понятие интеграла обобщается и на разрывные функции. 5.2
. Понятие интеграла обобщается и на разрывные функции. 5.2