6.1. Образец решения контрольных задач типового варианта.
Семестр 1.
Раздел I. Линейная и векторная алгебра. Аналитическая геометрия.
1 – 10. Вычислить определитель: 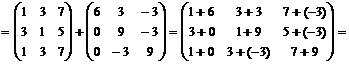

а) непосредственным разложением по  строке;
строке;
б) непосредственным разложением по  столбцу;
столбцу;
Решение.
а) вычисляем определитель разложением по элементам первой строки: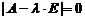
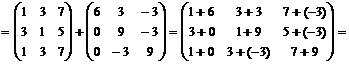 =
=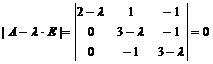 .
. 





Тогда  =
= =
=
б) вычисляем определитель непосредственным разложением по элементам
второго столбца: 
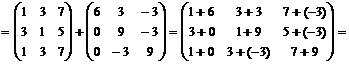 =
= .
.






Тогда  =
= =
= .
.
Ответ: 
 .
.
11-20. а) Найти матрицу  , если:
, если:
 ,
,  .
.
Решение:
1) Транспонируем матрицу 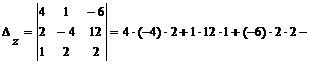 :
:  .
.
2) Вычисляем произведение матриц  :
:


 .
.
3) Находим матрицу  :
:

 .
.
4) Находим матрицу  :
: 

 .
.
б) Найти собственные числа матрицы  .
.
Множество собственных чисел матрицы совпадает с множеством корней характеристического уравнения матрицы 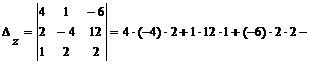 :
:  .
.
Решение:
Составляем характеристическое уравнение матрицы  :
:
 .
.
Записываем его в виде алгебраического уравнения и находим действительные корни (среди них могут быть и кратные):




 ,
,  .
.
Таким образом, собственными числами матрицы 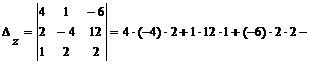 являются:
являются:  и
и  .
.
Ответ: а)  ; б)
; б) ,
,  .
.
21 – 30. Дана система уравнений:  . Требуется:
. Требуется:
а) найти решение системы методом Крамера; б) записать систему в матричном виде и найти её решение методом обратной матрицы; в) найти решение системы методом Гаусса.
Решение.
А) Метод Крамера.
1а) Вычисляем определитель системы и проверяем, что он отличен от нуля:

 .
.
2а) Так как  , то система имеет единственное решение, определяемое формулами Крамера:
, то система имеет единственное решение, определяемое формулами Крамера: 
3а) Вычисляем определители  :
:

 ,
,

 ,
,

 .
.
4а) Находим решение:  .
.
5а) Выполняем проверку: 
 .
.
Ответ:  .
.
Б) Метод обратной матрицы.
1б) Записываем систему уравнений в матричном виде:
 или
или 
2б) Вычисляем определитель системы и проверяем, что он отличен от нуля:


3б) Так как  , то матрица системы
, то матрица системы 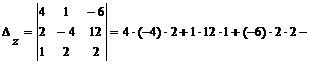 имеет обратную матрицу
имеет обратную матрицу  и единственное решение системы определяется формулой:
и единственное решение системы определяется формулой:
 или
или 
4б) Находим обратную матрицу  (методом присоединённой матрицы):
(методом присоединённой матрицы):
 .
.









Тогда  .
.
5б) Находим решение: 
 .
.
6б) Выполняем проверку: 
 .
.
Ответ:  .
.
В) Метод Гаусса.
1в) Записываем расширенную матрицу системы:
 .
.
2в) Выполняем прямой ход метода Гаусса.
В результате прямого хода матрица системы  должна быть преобразована с помощью элементарных преобразований строк к матрице
должна быть преобразована с помощью элементарных преобразований строк к матрице  треугольного или трапециевидного вида с элементами
треугольного или трапециевидного вида с элементами 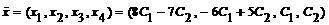 . Система уравнений, матрица которой
. Система уравнений, матрица которой  является треугольной с элементами
является треугольной с элементами 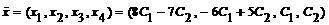
 , имеет единственное решение, а система уравнений, матрица которой
, имеет единственное решение, а система уравнений, матрица которой  является трапециевидной с элементами
является трапециевидной с элементами 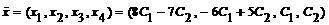
 , имеет бесконечно много решений.
, имеет бесконечно много решений.








 .
.
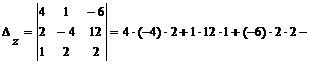 системы преобразована к специальному виду
системы преобразована к специальному виду 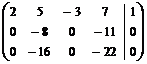 . Система уравнений, матрица которой
. Система уравнений, матрица которой 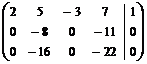 , является треугольной с ненулевыми диагональными элементами
, является треугольной с ненулевыми диагональными элементами 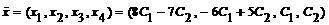 , имеет всегда единственное решение, которое находим, выполняя обратный ход.
, имеет всегда единственное решение, которое находим, выполняя обратный ход. Если при выполнение преобразования расширенной матрицы  в преобразованной матрице
в преобразованной матрице  появляется строка
появляется строка  , где
, где  , то это говорит о несовместности исходной системы уравнений.
, то это говорит о несовместности исходной системы уравнений.
3в) Выполняем обратный ход метода Гаусса.
Записываем систему уравнений, соответствующую последней расширенной матрице прямого хода:  и последовательно из уравнений системы, начиная с последнего, находим значения всех неизвестных:
и последовательно из уравнений системы, начиная с последнего, находим значения всех неизвестных: .
.
4в) Выполняем проверку: 
 .
.
Ответ:  .
.
31-40. Найти общее решение для каждой из данных систем методом Гаусса:
а)  .
.
Решение.
1а) Записываем расширенную матрицу системы:
 .
.
2а) Выполняем прямой ход метода Гаусса.

















 .
.
Матрица системы приведена к трапециевидному виду с ненулевыми диагональными элементами. Соответствующая такой матрице система уравнений имеет бесконечно много решений, которые находим, выполняя обратный ход, и записываем в виде общего решения. Для записи общего решения указываем её базисные и свободные неизвестные. Базисный минор матрицы системы образуют столбцы коэффициентов при неизвестных  и
и  :
:  . Поэтому выбираем в качестве базисных – неизвестные
. Поэтому выбираем в качестве базисных – неизвестные  и
и  , тогда свободными будут неизвестные
, тогда свободными будут неизвестные  и
и  .
.
3а) Выполняем обратный ход метода Гаусса.
Записываем систему уравнений, соответствующую последней расширенной матрице прямого хода:  . Свободным неизвестным придаём разные, произвольные постоянные значения:
. Свободным неизвестным придаём разные, произвольные постоянные значения:  ,
,  , и последовательно из уравнений системы, начиная с последнего, находим значения всех базисных неизвестных:
, и последовательно из уравнений системы, начиная с последнего, находим значения всех базисных неизвестных:  .
.
Тогда общее решение системы запишется в виде:  .
.
4а) Выполняем проверку:
 class="lazyload" data-src="/files/uch_group46/uch_pgroup327/uch_uch1418/image/597.gif">.
class="lazyload" data-src="/files/uch_group46/uch_pgroup327/uch_uch1418/image/597.gif">.
Ответ:  .
.
б)  .
.
Решение.
1а) Записываем расширенную матрицу системы:
 .
.
2а) Выполняем прямой ход метода Гаусса.








В результате прямого хода матрица системы  должна быть преобразована с помощью элементарных преобразований строк к матрице
должна быть преобразована с помощью элементарных преобразований строк к матрице треугольного или трапециевидного вида с элементами
треугольного или трапециевидного вида с элементами  .
.
Если, при выполнении преобразования расширенной матрицы  , в преобразованной матрице
, в преобразованной матрице  появляется строка
появляется строка  , где
, где  , то это говорит о несовместности исходной системы уравнений.
, то это говорит о несовместности исходной системы уравнений.
Для выполнения условия  может потребоваться перестановка местами столбцов матрицы системы. Если при выполнении преобразований прямого хода в матрице системы переставлялись местами столбцы коэффициентов при неизвестных, то в дальнейшем, при записи системы уравнений, соответствующей последней расширенной матрице прямого хода, это следует учесть.
может потребоваться перестановка местами столбцов матрицы системы. Если при выполнении преобразований прямого хода в матрице системы переставлялись местами столбцы коэффициентов при неизвестных, то в дальнейшем, при записи системы уравнений, соответствующей последней расширенной матрице прямого хода, это следует учесть.















 .
.
Матрица системы приведена к трапециевидному виду с ненулевыми диагональными элементами. Соответствующая такой матрице система уравнений имеет бесконечно много решений, которые находим, выполняя обратный ход, и записываем в виде общего решения. Для записи общего решения указываем её базисные и свободные неизвестные. Базисный минор матрицы системы, с учётом перестановки местами столбцов, образуют первый и второй столбцы коэффициентов при неизвестных  и
и  :
:  . Поэтому выбираем в качестве базисных – неизвестные
. Поэтому выбираем в качестве базисных – неизвестные  и
и  , тогда свободными будут неизвестные
, тогда свободными будут неизвестные  и
и  .
.
3б) Выполняем обратный ход метода Гаусса.
Записываем систему уравнений, соответствующую последней расширенной матрице прямого хода:  . Свободным неизвестным придаём разные, произвольные постоянные значения:
. Свободным неизвестным придаём разные, произвольные постоянные значения:  ,
,  , и последовательно из уравнений системы, начиная с последнего, находим значения всех базисных неизвестных:
, и последовательно из уравнений системы, начиная с последнего, находим значения всех базисных неизвестных:  .
.
Тогда общее решение системы запишется в виде:

4б) Выполняем проверку:



Ответ:  .
.
в)  .
.
Решение.
1в) Записываем расширенную матрицу системы:
 .
.
2в) Выполняем прямой ход метода Гаусса.










 .
.
При выполнении преобразования расширенной матрицы  , в преобразованной матрице
, в преобразованной матрице  появилась строка
появилась строка  , соответствующая уравнению
, соответствующая уравнению  , которому не удовлетворяет ни один набор значений неизвестных
, которому не удовлетворяет ни один набор значений неизвестных  , что говорит о несовместности исходной системы уравнений.
, что говорит о несовместности исходной системы уравнений.
Ответ: Система несовместна.
41 – 50. Даны векторы  :
:  ;
;  ;
;  ;
;  . Показать, что векторы
. Показать, что векторы  образуют базис
образуют базис  и найти координаты вектора
и найти координаты вектора  в этом базисе.
в этом базисе.
Решение.
1) Покажем, что векторы  образуют базис
образуют базис  . Для этого составим определитель, столбцами которого являются координаты этих векторов и покажем, что он отличен от нуля.
. Для этого составим определитель, столбцами которого являются координаты этих векторов и покажем, что он отличен от нуля.
 .
.
Так как  , то векторы
, то векторы  образуют базис
образуют базис  и, следовательно, вектор
и, следовательно, вектор  единственным образом можно разложить по векторам этого базиса.
единственным образом можно разложить по векторам этого базиса.
2) Записываем разложение вектора  по векторам базиса
по векторам базиса  :
:
 или
или  .
.
Коэффициенты разложения  ,
,  ,
,  называют координатами вектора
называют координатами вектора  в базисе
в базисе  и записывают:
и записывают:  .
.
3) Записываем векторное уравнение относительно  ,
, ,
, в виде эквивалентной ему системы линейных уравнений:
в виде эквивалентной ему системы линейных уравнений: , и находим
, и находим
единственное решение системы, например, по формулам Крамера:
 , где
, где
 ,
, ,
, ,
, .
.
Таким образом:  ,
,  ,
,  . Следовательно, разложение имеет вид:
. Следовательно, разложение имеет вид:  или кратко:
или кратко:  .
.
Ответ:  .
.
51 – 60. Даны векторы  :
:  ,
,  ,
,  . Требуется: а) найти векторы
. Требуется: а) найти векторы  и
и  ; б) вычислить скалярное произведение
; б) вычислить скалярное произведение  ; в) найти проекцию вектора
; в) найти проекцию вектора  на направление вектора
на направление вектора  ; г) найти векторное произведение
; г) найти векторное произведение  и его модуль
и его модуль  .
.
Решение.
a) Находим векторы  и
и  :
:


=
 ;
;


=class="lazyload" data-src="/files/uch_group46/uch_pgroup327/uch_uch1418/image/665.gif"> .
.
б) Вычисляем скалярное произведение векторов  :
:
 .
.
в) Находим проекцию вектора  на направление вектора
на направление вектора  :
:
 .
.
г) Находим векторное произведение векторов  :
:



и вычисляем его модуль:  =
= .
.
Ответ: а) =
= ;
;  =
= ; б)
; б)  ; в)
; в)  ; г)
; г) 
 ,
, 
 .
.
61-70. Даны вершины треугольника  :
:  ,
,  ,
,  Требуется найти:
Требуется найти:
а) длину стороны  ; б) уравнение стороны
; б) уравнение стороны  ;
;
в) уравнение медианы  , проведённой из вершины
, проведённой из вершины  ;
;
г) уравнение высоты  , проведённой из вершины
, проведённой из вершины  ;
;
д) длину  высоты
высоты  ; е) площадь
; е) площадь  треугольника
треугольника  . Сделать чертёж.
. Сделать чертёж.
Решение. Сделаем чертёж:

а) Длину стороны  находим как длину вектора
находим как длину вектора  :
:
 ,
,
 .
.
б) Уравнение стороны  находим как уравнение прямой, проходящей через точки
находим как уравнение прямой, проходящей через точки  и
и  , и записываем его в виде общего уравнения прямой:
, и записываем его в виде общего уравнения прямой:







 .
.
в) Уравнение медианы  находим как уравнение прямой, проходящей через точки
находим как уравнение прямой, проходящей через точки  и
и  , и записываем его в виде общего уравнения прямой. Неизвестные координаты точки
, и записываем его в виде общего уравнения прямой. Неизвестные координаты точки  находим как координаты точки, делящей сторону
находим как координаты точки, делящей сторону  пополам:
пополам:
 ;
;  .
.
Тогда:






 .
.
г) Уравнение высоты  находим как уравнение прямой, проходящей через точку
находим как уравнение прямой, проходящей через точку  перпендикулярно вектору
перпендикулярно вектору  , который принимаем за нормальный вектор прямой
, который принимаем за нормальный вектор прямой  . Тогда
. Тогда 



д) Длину  высоты
высоты  находим как расстояние от точки
находим как расстояние от точки  до прямой
до прямой  , заданной общим уравнением
, заданной общим уравнением  :
:
 .
.
е) Площадь треугольника  находим по формуле:
находим по формуле:  . Откуда
. Откуда  .
.
Ответ: а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  ; е)
; е)  .
.
71 – 80. Даны вершины пирамиды  . Требуется найти:
. Требуется найти:
а) длины ребер  и
и  ; б) угол между ребрами
; б) угол между ребрами  и
и  ;
;
в) площадь грани  ; г) объем пирамиды
; г) объем пирамиды  ;
;
д) уравнение плоскости грани  ; е) длину
; е) длину  высоты
высоты  пирамиды.
пирамиды.
Решение.
а) Длины рёбер  и
и  находим как длины векторов
находим как длины векторов  и
и  :
:
 ;
;
 ;
;
 ;
;
 .
.
б) Угол  между рёбрами
между рёбрами  и
и  находим как угол между векторами
находим как угол между векторами  и
и  по формуле:
по формуле:  . Учитывая, что:
. Учитывая, что:  ,
,  ,
,  получим
получим  . Откуда
. Откуда 
в) Площадь  грани
грани  находим, используя геометрический смысл векторного произведения векторов, по формуле
находим, используя геометрический смысл векторного произведения векторов, по формуле  . Учитывая, что:
. Учитывая, что: 
 ,
,  , получим
, получим  .
.
г) Объём  пирамиды
пирамиды  находим, используя геометрический смысл смешанного произведения векторов, по формуле
находим, используя геометрический смысл смешанного произведения векторов, по формуле  . Учитывая, что:
. Учитывая, что:
 ,
,
 ,
,
получим  .
.
д) Уравнение плоскости грани  находим как уравнение плоскости, проходящей через точки
находим как уравнение плоскости, проходящей через точки  ,
,  и
и  , и записываем его в виде общего уравнения плоскости:
, и записываем его в виде общего уравнения плоскости:







е) Длину  высоты
высоты  пирамиды
пирамиды  находим как расстояние от точки
находим как расстояние от точки  до плоскости
до плоскости  , заданной общим уравнением
, заданной общим уравнением  :
:
 .
.
Ответ: а)  ,
,  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  ; е)
; е)  .
.
81–90. Установить, какую невырожденную кривую определяет алгебраическое уравнение второго порядка, построить её:
а)  ; б)
; б)  ;
;
в)  .
.
Решение:
а) Так как  ,
,  , то уравнение определяет гиперболу с центром в точке
, то уравнение определяет гиперболу с центром в точке  и осями симметрии, параллельными координатным осям:
и осями симметрии, параллельными координатным осям:  . Вид кривой и расположение её на плоскости известны. Выделяя полные квадраты в левой части уравнения
. Вид кривой и расположение её на плоскости известны. Выделяя полные квадраты в левой части уравнения  , преобразуем его следующим образом:
, преобразуем его следующим образом:





 .
.
Полученное уравнение определяет гиперболу с центром в точке  и осями симметрии параллельными координатным осям. Для построения гиперболы в системе координат
и осями симметрии параллельными координатным осям. Для построения гиперболы в системе координат  : 1) отмечаем центр гиперболы
: 1) отмечаем центр гиперболы  ; 2) проводим через центр
; 2) проводим через центр  пунктиром оси симметрии гиперболы; 3) строим пунктиром основной прямоугольник гиперболы с центром
пунктиром оси симметрии гиперболы; 3) строим пунктиром основной прямоугольник гиперболы с центром  и сторонами
и сторонами  и
и  параллельными осям симметрии; 4) проводим через противоположные вершины основного прямоугольника пунктиром прямые, являющиеся асимптотами гиперболы, к которым неограниченно близко при бесконечном удалении от начала координат приближаются ветви гиперболы, не пересекая их; 5) изображаем сплошной линией ветви гиперболы (рис. 1).
параллельными осям симметрии; 4) проводим через противоположные вершины основного прямоугольника пунктиром прямые, являющиеся асимптотами гиперболы, к которым неограниченно близко при бесконечном удалении от начала координат приближаются ветви гиперболы, не пересекая их; 5) изображаем сплошной линией ветви гиперболы (рис. 1).
Ответ: Гипербола с центром в точке  (см. рис.1)..
(см. рис.1)..

Рис.1
б) Так как  ,
,  ,
,  , то уравнение определяет эллипс с центром в точке
, то уравнение определяет эллипс с центром в точке  и осями симметрии, параллельными координатным осям:
и осями симметрии, параллельными координатным осям:  . Вид кривой и расположение её на плоскости известны. Выделяя полные квадраты в левой части
. Вид кривой и расположение её на плоскости известны. Выделяя полные квадраты в левой части
уравнения  , преобразуем его следующим образом:
, преобразуем его следующим образом: 




 .
.
Полученное уравнение определяет эллипс с центром в точке  и осями симметрии параллельными осям координат. Для построения эллипса в системе координат
и осями симметрии параллельными осям координат. Для построения эллипса в системе координат  : 1) отмечаем центр эллипса
: 1) отмечаем центр эллипса  ; 2) проводим через центр
; 2) проводим через центр  пунктиром оси симметрии эллипса; 3) строим пунктиром основной прямоугольник эллипса с центром
пунктиром оси симметрии эллипса; 3) строим пунктиром основной прямоугольник эллипса с центром  и сторонами
и сторонами  и
и  параллельными осям симметрии; 4) изображаем сплошной линией эллипс, вписывая его в основной прямоугольник так, чтобы эллипс касался его сторон в точках пересечения прямоугольника с осями симметрии (рис.2).
параллельными осям симметрии; 4) изображаем сплошной линией эллипс, вписывая его в основной прямоугольник так, чтобы эллипс касался его сторон в точках пересечения прямоугольника с осями симметрии (рис.2).
Ответ: Эллипс с центром в точке  (см. рис.2).
(см. рис.2).
в) Так как  ,
,  ,
,  , то уравнение определяет параболу с вершиной в точке
, то уравнение определяет параболу с вершиной в точке  и осью симметрии, параллельной координатной оси
и осью симметрии, параллельной координатной оси  :
:  . Вид кривой и расположение её на плоскости известны. Выделяя полные квадраты в левой части уравнения
. Вид кривой и расположение её на плоскости известны. Выделяя полные квадраты в левой части уравнения  , преобразуем его следующим образом:
, преобразуем его следующим образом:






Полученное уравнение определяет параболу с вершиной в точке  и осью симметрии параллельной оси
и осью симметрии параллельной оси  . Для построения параболы в системе координат
. Для построения параболы в системе координат  : 1) отмечаем вершину параболы
: 1) отмечаем вершину параболы  ; 2) проводим через вершину
; 2) проводим через вершину  пунктиром ось симметрии параболы; 3) изображаем сплошной линией параболу, направляя её ветвь, с учётом того, что параметр параболы
пунктиром ось симметрии параболы; 3) изображаем сплошной линией параболу, направляя её ветвь, с учётом того, что параметр параболы  , в положительную сторону оси
, в положительную сторону оси  (рис.3).
(рис.3).
Ответ: Парабола с вершиной в точке  (см. рис.3).
(см. рис.3).

Рис.2. Рис.3.
91-100. Имеются данные о работе трёх отраслей экономики в отчётном периоде и план выпуска конечной продукции  в следующем периоде (в усл. ден. ед.). Требуется, используя модель Леонтьева многоотраслевой экономики, найти: а) матрицы коэффициентов прямых и полных затрат; б) плановые объёмы выпуска валовой продукции каждой из отраслей, межотраслевые поставки и объёмы выпуска чистой продукции. В ответе записать данные межотраслевого баланса планового периода. (Указание: значения коэффициентов прямых и полных затрат вычислить с точностью до 0.01; значения плановых объёмов выпуска валовой и чистой продукции, межотраслевых поставок округлить до целых значений).
в следующем периоде (в усл. ден. ед.). Требуется, используя модель Леонтьева многоотраслевой экономики, найти: а) матрицы коэффициентов прямых и полных затрат; б) плановые объёмы выпуска валовой продукции каждой из отраслей, межотраслевые поставки и объёмы выпуска чистой продукции. В ответе записать данные межотраслевого баланса планового периода. (Указание: значения коэффициентов прямых и полных затрат вычислить с точностью до 0.01; значения плановых объёмов выпуска валовой и чистой продукции, межотраслевых поставок округлить до целых значений).
| Отрасли производства | Отрасти потребления | Конечный продукт | Валовой продукт | ||
| I | II | III | |||
| I | 20 | 25 | 105 | 50 | 200 |
| II | 60 | 75 | 70 | 45 | 250 |
| III | 60 | 50 | 140 | 100 | 350 |
| Чистый продукт | 60 | 100 | 35 | ||
| Валовой продукт | 200 | 250 | 350 | ||
Решение.
1) Находим матрицу  коэффициентов прямых затрат
коэффициентов прямых затрат  (
( - номер отрасли производства,
- номер отрасли производства,  - номер отрасли потребления) и устанавливаем её продуктивность:
- номер отрасли потребления) и устанавливаем её продуктивность:
 ,
,  ,
, 
 ,
,  ,
, 
 ,
,  ,
,  .
.
Таким образом  .
.
Так как  (
( ) и
) и  , то матрица
, то матрица 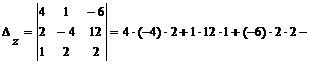 продуктивна и, следовательно, для любого
продуктивна и, следовательно, для любого  существует решение
существует решение  уравнения Леонтьева:
уравнения Леонтьева:  , записываемое в виде
, записываемое в виде  , где
, где  - единичная матрица,
- единичная матрица,  - матрица коэффициентов полных затрат,
- матрица коэффициентов полных затрат,  и
и  - векторы (матрицы-столбцы) валового выпуска и конечного продукта, соответственно .
- векторы (матрицы-столбцы) валового выпуска и конечного продукта, соответственно .
2а) Находим матрицу:
 .
.
3а) Находим матрицу  , обратную к
, обратную к  , методом
, методом
присоединённой матрицы, по формуле:  ,
,
где:


 ,
,


 ,
,


 ,
,
 .
.
Тогда  .
.
1б) Находим вектор  валового выпуска на вектор
валового выпуска на вектор  конечного продукта в плановом периоде, следующим за отчётным (в предположении, что матрица
конечного продукта в плановом периоде, следующим за отчётным (в предположении, что матрица 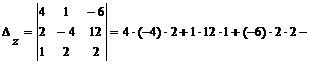 , называемая также технологической, а, следовательно, и матрица
, называемая также технологической, а, следовательно, и матрица  не изменяются, т.е.
не изменяются, т.е.  ) по формуле:
) по формуле:
 .
.
2б) Находим по формуле  (
( ) плановые межотраслевые поставки
) плановые межотраслевые поставки  , округляя полученные значения до целых (с учётом балансовых соотношений
, округляя полученные значения до целых (с учётом балансовых соотношений  ,
,  ):
):
 ,
,  ,
,  ,
,
 ,
,  ,
,  ,
,  ,
,  ,
,  .
.
3б) Плановые объёмы 
 выпуска чистой продукции каждой из отраслей находим по формуле
выпуска чистой продукции каждой из отраслей находим по формуле 
 :
:
 ,
,  ,
,
 .
.
Ответ: Межотраслевой баланс планового периода имеет вид:
| Отрасли производства | Отрасти потребления | Конечный продукт | Валовой продукт | ||
| I | II | III | |||
| I | 20 | 27 | 97 | 60 | 204 |
| II | 61 | 80 | 65 | 60 | 266 |
| III | 61 | 53 | 130 | 80 | 324 |
| Чистый продукт | 62 | 106 | 32 | ||
| Валовой продукт | 204 | 266 | 324 | ||
Раздел II. Введение в математический анализ. Дифференциальное
исчисление функции одной переменной.
101-110. Требуется:
а) найти естественную область определения функции  ;
;
б) установить чётность (нечётность) функции  .
.
Решение.
а) Естественную область определения находим как множество  всех значений аргумента
всех значений аргумента  функции, для которых формула
функции, для которых формула  имеет смысл:
имеет смысл:  . Решив (на числовой прямой) систему неравенств
. Решив (на числовой прямой) систему неравенств  , устанавливаем, что геометрическим образом множества
, устанавливаем, что геометрическим образом множества  является промежуток
является промежуток  .
.
б) Находим сначала естественную область определения функции  :
:  . Решив (на числовой прямой) неравенство
. Решив (на числовой прямой) неравенство  , устанавливаем, что геометрическим образом множества
, устанавливаем, что геометрическим образом множества  является объединение промежутков
является объединение промежутков  .
.
Так как область  является симметричной относительно точки
является симметричной относительно точки  , то проверяем выполнение для всех
, то проверяем выполнение для всех  условий:
условий:  или
или  , учитывая чётность и нечётность основных элементарных функций, входящих в аналитическое выражение
, учитывая чётность и нечётность основных элементарных функций, входящих в аналитическое выражение  .
.
Если область  не симметрична относительно точки
не симметрична относительно точки  , то
, то  на этом множестве является функцией общего вида.
на этом множестве является функцией общего вида.
Для этого находим  . Поскольку
. Поскольку  для всех
для всех 

 , то функция
, то функция  является чётной.
является чётной.
Ответ: а) 
 ,
,  ;
;
б) функция  - чётная.
- чётная.
111-120. Даны комплексные числа  ,
, и алгебраическое уравнение
и алгебраическое уравнение  . Требуется: а) вычислить
. Требуется: а) вычислить ,
,  ,
,  ,
,  ; б) найти все корни алгебраического уравнения на множестве комплексных чисел.
; б) найти все корни алгебраического уравнения на множестве комплексных чисел.
Решение.
1а) Вычисляем  :
:  .
.
2а) Вычисляем  .
.
Сначала находим  . Тогда
. Тогда 

 .
.
3а) Вычисляем  .
.
Сначала находим 

 (учитываем, что
(учитываем, что  )
) . Тогда
. Тогда 

4а) Вычисляем  :
: 
 (учитываем, что
(учитываем, что  )
) .
.
1б) Для нахождения корней алгебраического уравнения  , раскладываем его левую часть на множители:
, раскладываем его левую часть на множители:
 .
.
2б) Находим корни уравнения на множестве комплексных чисел, приравнивая каждый из множителей нулю (число корней, с учётом кратности, должно равняться порядку уравнения):
1) 

 .
.
2) 

 .
.
3)  . Так как дискриминант квадратного уравнения
. Так как дискриминант квадратного уравнения  , то уравнение имеет два комплексно-сопряжённых корня:
, то уравнение имеет два комплексно-сопряжённых корня:  .
.
Корни  ,
,  можно найти и как корни уравнения
можно найти и как корни уравнения  , по формуле
, по формуле  . Для нахождения комплексных значений корня, число
. Для нахождения комплексных значений корня, число  следует представить в виде комплексного числа в тригонометрической форме:
следует представить в виде комплексного числа в тригонометрической форме:  , после чего значения корня найти по формуле:
, после чего значения корня найти по формуле:  ,где
,где 
Ответ:
a)  ,
, 
 ,
,  ,
,  ;
;
б)  ,
,  ,
,  .
.
121-130. Вычислить пределы (не пользуясь правилом Лопиталя):
а)  б)
б)  в)
в) 
г)  д)
д) 
Вычисление предела  , где
, где  , начинают всегда с подстановки в
, начинают всегда с подстановки в  предельного значения её аргумента
предельного значения её аргумента  . В результате могут получиться неопределённости
. В результате могут получиться неопределённости  ,
,  ,
,  , которые раскрывают тождественными преобразованиями
, которые раскрывают тождественными преобразованиями  такими, чтобы преобразованное выражение получилось определённым. При вычислении пределов используют свойства конечных пределов и бесконечно больших функций, а также следующие известные пределы:
такими, чтобы преобразованное выражение получилось определённым. При вычислении пределов используют свойства конечных пределов и бесконечно больших функций, а также следующие известные пределы: 
 ,
,  ,
,  (
( ),
),  ,
,  ,
,  ,
,  ,
,  .
.
Решение. а)  При подстановке вместо переменной
При подстановке вместо переменной  её предельного значения
её предельного значения  получим неопределённость
получим неопределённость  . Для её раскрытия сначала разделим числитель и знаменатель дроби на
. Для её раскрытия сначала разделим числитель и знаменатель дроби на  (старшую степень переменной
(старшую степень переменной  в числителе и знаменателе), после чего используем свойства конечных пределов и бесконечно больших функций. Получим
в числителе и знаменателе), после чего используем свойства конечных пределов и бесконечно больших функций. Получим 


 .
.
б)  При подстановке вместо переменной
При подстановке вместо переменной  её предельного значения
её предельного значения  получим неопределённость
получим неопределённость  . Для её раскрытия выделим в числителе и знаменателе дроби общий множитель вида
. Для её раскрытия выделим в числителе и знаменателе дроби общий множитель вида  , где
, где  - некоторое число, т.е. множитель
- некоторое число, т.е. множитель  . Затем сократим на него числитель и знаменатель дроби, после чего используем свойства пределов.
. Затем сократим на него числитель и знаменатель дроби, после чего используем свойства пределов.
1) В квадратном трёхчлене  множитель выделяют разложением квадратного трёхчлена по формуле
множитель выделяют разложением квадратного трёхчлена по формуле  , где
, где  . 2) В выражении
. 2) В выражении  множитель выделяют следующим способом:
множитель выделяют следующим способом: 

 .
.
В результате получим 



 .
.
в)  При подстановке вместо переменной
При подстановке вместо переменной  её предельного значения
её предельного значения  получим неопределённость
получим неопределённость  . Выделим в числителе множители вида
. Выделим в числителе множители вида  , где
, где  при
при  и используем свойства пределов. Получим
и используем свойства пределов. Получим



Для раскрытия неопределённостей  , содержащих тригонометрические и обратные тригонометрические функции, в числителе и знаменателе дроби выделяют сначала множители вида:
, содержащих тригонометрические и обратные тригонометрические функции, в числителе и знаменателе дроби выделяют сначала множители вида:  ,
, ,
,  ,
, , где
, где  при
при  , используя формулы тригонометрии:
, используя формулы тригонометрии:  ,
,  ,
,  .
.
После чего применяют свойства пределов, учитывая, что:
 ,
,  ,
,  ,
,  .
.


 .
.
г)  При подстановке вместо переменной
При подстановке вместо переменной  её предельного значения
её предельного значения  получим неопределённость
получим неопределённость  .
.
Для раскрытия неопределённости  , возникающей при вычислении предела
, возникающей при вычислении предела  , где
, где  ,
,  , сначала выражение
, сначала выражение  представляют в виде
представляют в виде  , где
, где  при
при  . После чего используют свойства пределов, заменяя выражение
. После чего используют свойства пределов, заменяя выражение  его предельным значением
его предельным значением  и учитывая, что
и учитывая, что  =
= .
.
Представим  в виде
в виде  , где
, где  при
при  ,следующим способом:
,следующим способом:

 =
= . Тогда учитывая, что
. Тогда учитывая, что  ,
,
 , получим
, получим  =
=
 =
= .
.
д) 
Для вычисления предела  , где
, где  представляет собой дробь, числитель и знаменатель которой содержат факториалы натурального числа
представляет собой дробь, числитель и знаменатель которой содержат факториалы натурального числа  , поступают следующим образом. Выделяют в числителе и знаменателе в качестве общего множителя факториал меньшего натурального числа и сокращают на него. В результате получают выражение, предел которого находят рассмотренными выше способами.
, поступают следующим образом. Выделяют в числителе и знаменателе в качестве общего множителя факториал меньшего натурального числа и сокращают на него. В результате получают выражение, предел которого находят рассмотренными выше способами.
Для вычисления данного предела сначала выразим  ,
,  ,
,  через
через  :
:  ,
,  ,
,  , после чего сократим числитель и знаменатель на
, после чего сократим числитель и знаменатель на  :
: 


 .
.
В результате получили неопределённость  . Для её раскрытия разделим числитель и знаменатель дроби
. Для её раскрытия разделим числитель и знаменатель дроби  на
на  (старшую степень переменной
(старшую степень переменной  числителя и знаменателя), после чего используем свойства пределов. Получим
числителя и знаменателя), после чего используем свойства пределов. Получим 


 .
.
Ответ: а) ; б)
; б) ; в)
; в) ; г)
; г) ; д)
; д) .
.
131-140. Для указанной функции  требуется: а) выяснить при каких значениях параметра
требуется: а) выяснить при каких значениях параметра  функция будет непрерывной; б) найти точки разрыва функции и исследовать их характер. Построить график функции.
функция будет непрерывной; б) найти точки разрыва функции и исследовать их характер. Построить график функции.
а)  ; б)
; б)  .
.
Решение.
Точками разрыва функции  являются точки разрыва функций
являются точки разрыва функций  в промежутках
в промежутках  ,
,  ,…,
,…, , кроме того, точками возможного разрыва функции
, кроме того, точками возможного разрыва функции  являются точки
являются точки  в окрестности которых и в самих точках функция задаётся разными аналитическими выражениями.
в окрестности которых и в самих точках функция задаётся разными аналитическими выражениями.
Точка  является точкой непрерывности функции
является точкой непрерывности функции  тогда и только тогда, когда:
тогда и только тогда, когда:  .
.
а) Поскольку функции  и
и  непрерывны в промежутках
непрерывны в промежутках  и
и  как элементарные функции, определённые в каждой точке данных промежутков, то непрерывность функции
как элементарные функции, определённые в каждой точке данных промежутков, то непрерывность функции  может нарушиться только в точке её возможного разрыва
может нарушиться только в точке её возможного разрыва  .
.
Определяем значение параметра  из условия непрерывности функции
из условия непрерывности функции  в точке
в точке  :
:  . Вычисляя
. Вычисляя  ,
,  ,
,  :
:  ,
,  ,
,  , из условия непрерывности
, из условия непрерывности  , находим
, находим  .
.
График непрерывной функции  имеет вид изображённый на рис. 4.
имеет вид изображённый на рис. 4.
б) Функции  и
и  непрерывны в промежутках
непрерывны в промежутках  и
и  как элементарные функции, определённые в каждой точке данных промежутков, а функция
как элементарные функции, определённые в каждой точке данных промежутков, а функция  в промежутке
в промежутке  имеет точкой разрыва точку
имеет точкой разрыва точку  , в которой она не определена. Тогда для функции
, в которой она не определена. Тогда для функции  точка
точка  является точкой разрыва, а точки
является точкой разрыва, а точки  и
и  , в окрестности которых и в самих точках функция задаётся разными аналитическими выражениями, являются точками возможного разрыва.
, в окрестности которых и в самих точках функция задаётся разными аналитическими выражениями, являются точками возможного разрыва.
Исследуем на разрыв точки  и установим характер разрыва:
и установим характер разрыва:
1) 



 .
.
Следовательно, точка  - точка разрыва 1-го рода функции
- точка разрыва 1-го рода функции  .
.
2) 
 . Следовательно, точка
. Следовательно, точка  - точка бесконечного разрыва (2-го рода) функции
- точка бесконечного разрыва (2-го рода) функции  .
.
3) 



 .
.
Следовательно, точка  - точка непрерывности функции
- точка непрерывности функции  .
.
График функции  имеет вид, изображённый на рис.5.
имеет вид, изображённый на рис.5.
Ответ: а) Функция  непрерывна при
непрерывна при  (рис.4); б)
(рис.4); б)  - точка разрыва 1-го рода,
- точка разрыва 1-го рода,  - точка бесконечного разрыва функции
- точка бесконечного разрыва функции  (рис.5).
(рис.5). 


Рис.4 Рис.5
141-150. Найти производную  :
:
а)  ; б)
; б)  ; в)
; в) .
.
Нахождение производной  функции
функции  заданной явно, с помощью правил дифференцирования:
заданной явно, с помощью правил дифференцирования:
 (
( ),
),  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  сводят к нахождению табличных производных (приложение 6.3).
сводят к нахождению табличных производных (приложение 6.3).
Производную  функции
функции  заданной параметрическими уравнениями
заданной параметрическими уравнениями  находят в параметрическом виде по формуле
находят в параметрическом виде по формуле  .
.
Решение.
а)  , где
, где

 =
= ;
; 



Тогда  .
.
б)  , где
, где




 .
.



 .
.
Тогда 
 .
.
в) Производную функции  , заданной параметрическими уравнениями
, заданной параметрическими уравнениями  находим по формуле
находим по формуле  , где
, где



 ;
;


 .
.
Тогда  .
.
151-160. Вычислить пределы, используя правило Лопиталя.
а) ; б)
; б)  ; в)
; в)  .
.
Вычисление предела , где
, где  , всегда начинают с подстановки в
, всегда начинают с подстановки в  предельного значения её аргумента
предельного значения её аргумента  . Если в результате получают неопределённость
. Если в результате получают неопределённость  или
или  , то для её раскрытия применяют правило Лопиталя:
, то для её раскрытия применяют правило Лопиталя:  , где
, где  и
и - функции, дифференцируемые в окрестности
- функции, дифференцируемые в окрестности  . В некоторых случаях может потребоваться неоднократное применение данного правила. На каждом этапе его применения следует использовать, упрощающие отношение, тождественные преобразования, а также комбинировать это правило с любыми другими известными приёмами вычисления пределов. Раскрытие неопределённостей вида:
. В некоторых случаях может потребоваться неоднократное применение данного правила. На каждом этапе его применения следует использовать, упрощающие отношение, тождественные преобразования, а также комбинировать это правило с любыми другими известными приёмами вычисления пределов. Раскрытие неопределённостей вида:  ,
,  ,
,  ,
,  ,
,  путём преобразований:
путём преобразований:  ,
, ,
, сводят к раскрытию неопределенностей вида
сводят к раскрытию неопределенностей вида  или
или  .
.
Решение.
а) 
 , где
, где


 ,
,



Тогда 
 .
.
б) 
 , где
, где




 ,
,


 .
.
Тогда 
 . Применяем правило Лопиталя ещё раз:
. Применяем правило Лопиталя ещё раз:
 , где
, где


 ,
,


 =
=
 .
.
Тогда 
 .
.
в)  . Преобразуем данную неопределённость (приведением разности дробей к общему знаменателю) к виду
. Преобразуем данную неопределённость (приведением разности дробей к общему знаменателю) к виду  , после чего применим правило Лопиталя. Получим
, после чего применим правило Лопиталя. Получим 
=
 , где
, где


 ,
,


 .
.
Тогда 

 .
.
Применяем правило Лопиталя ещё раз:

 , где
, где 

 ,
,



 .
.
В итоге получим 
 .
.
Ответ:
а) ; б)
; б) ; в)
; в) .
.
161-170. Провести полное исследование функции 
 и построить её график.
и построить её график.
Для построения графика функции  нужно:
нужно:
1) найти область определения функции;
2) найти область непрерывности функции и точки разрыва;
3) исследовать функцию на чётность, нечётность и периодичность;
4) найти точки пересечения графика с осями координат;
5) найти асимптоты графика функции;
6) найти интервалы возрастания и убывания, экстремумы функции;
7) найти интервалы выпуклости, вогнутости и точки перегиба.
Решение.
1) Находим область определения функции:  =
= ).
).
2) Поскольку данная функция является элементарной, то областью её непрерывности является область определения  , а точками разрыва являются точки
, а точками разрыва являются точки  и
и  , не принадлежащие множеству
, не принадлежащие множеству , но являющиеся предельными точками этого множества (точками в любой окрестности которых содержатся точки данного множества). Исследуем характер разрыва в точках
, но являющиеся предельными точками этого множества (точками в любой окрестности которых содержатся точки данного множества). Исследуем характер разрыва в точках и
и  , вычислив в них односторонние пределы функции:
, вычислив в них односторонние пределы функции:
 ,
,  ,
,
 ,
,  .
.
Так как односторонние пределы функции в точках  и
и  - бесконечные, то данные точки являются точками бесконечного разрыва.
- бесконечные, то данные точки являются точками бесконечного разрыва.
3) Функция не является периодической.
Функция  , в аналитическое выражение которой входит хотя бы одна непериодическая функция периодической не является.
, в аналитическое выражение которой входит хотя бы одна непериодическая функция периодической не является.
Проверяем является ли функция чётной или нечётной. Так как область определения функции  =
= ) не симметрична относительно точки
) не симметрична относительно точки  , то данная функция – общего вида.
, то данная функция – общего вида.
4) Находим точки пересечения графика с осями координат.
Так как  , то точек пересечения графика с осью
, то точек пересечения графика с осью  нет.
нет.
Положим и решим уравнение
и решим уравнение  . Его решением является
. Его решением является  . Следовательно, точка
. Следовательно, точка - точка пересечения графика с осью
- точка пересечения графика с осью  .
.
5) Находим вертикальные и наклонные асимптоты графика функции.
Прямая  является вертикальной асимптотой, тогда и только тогда, когда
является вертикальной асимптотой, тогда и только тогда, когда  является точкой бесконечного разрыва функции
является точкой бесконечного разрыва функции  .
.
Так как точки  и
и  - точки бесконечного разрыва данной функции, то вертикальными асимптотами графика функции являются прямые
- точки бесконечного разрыва данной функции, то вертикальными асимптотами графика функции являются прямые  и
и  .
.
Прямая  является наклонной асимптотой графика функции
является наклонной асимптотой графика функции  при
при  тогда и только тогда, когда одновременно существуют конечные пределы:
тогда и только тогда, когда одновременно существуют конечные пределы: и
и  .
.
Вычисляем сначала пределы при  :
:
 ,
, .
.
В дальнейшем будем иметь в виду следующий часто встречающийся предел:
Следовательно  , т.е.
, т.е.  - наклонная (горизонтальная) асимптота графика функции при
- наклонная (горизонтальная) асимптота графика функции при  .
.
Аналогично вычисляем пределы при  :
:  ,class="lazyload" data-src="/files/uch_group46/uch_pgroup327/uch_uch1418/image/1233.gif"> Следовательно
,class="lazyload" data-src="/files/uch_group46/uch_pgroup327/uch_uch1418/image/1233.gif"> Следовательно  , т.е.
, т.е.  - наклонная (горизонтальная) асимптота графика функции при
- наклонная (горизонтальная) асимптота графика функции при  .
.
6) Определяем интервалы возрастания, убывания, экстремумы функции. Для этого находим первую производную функции:



и определяем критические точки функции  , т.е. точки
, т.е. точки  в которых
в которых  или
или  не существует:
не существует:




 ;
;
 не существует при
не существует при 

 и
и  .
.
Таким образом, единственной критической (стационарной) точкой функции  является точка
является точка  .
.
Исследуем знак производной  в интервалах, на которые критические точки функции
в интервалах, на которые критические точки функции  разбивают её область определения
разбивают её область определения  , и найдём интервалы возрастания, убывания, экстремумы функции. Результаты исследования представим следующей таблицей:
, и найдём интервалы возрастания, убывания, экстремумы функции. Результаты исследования представим следующей таблицей:
 |  |  |  |  |  |
 | + | + |  |  |  |
 | возрастает | возрастает |  | убывает | убывает |
Так как при переходе слева направо через точку производная
производная  меняет знак с «+» на «
меняет знак с «+» на « », то точка
», то точка  является точкой локального максимума и
является точкой локального максимума и  .
.
7) Определяем интервалы выпуклости, вогнутости, точки перегиба графика функции. Для этого находим вторую производную функции:


и определяем точки возможного перегиба  , т.е. точки
, т.е. точки  в которых
в которых или
или не существует:
не существует: , так как
, так как  (квадратное уравнение не имеет действительных корней);
(квадратное уравнение не имеет действительных корней);  не существует при
не существует при 

 и
и  .
.
Таким образом, функция  не имеет точек возможного перегиба.
не имеет точек возможного перегиба.
Исследуем знак второй производной  в интервалах, на которые точки возможного перегиба функции
в интервалах, на которые точки возможного перегиба функции  разбивают её область определения
разбивают её область определения  , и найдём интервалы выпуклости, вогнутости, точки перегиба графика функции. Результаты исследования представим таблицей:
, и найдём интервалы выпуклости, вогнутости, точки перегиба графика функции. Результаты исследования представим таблицей:
 |  |  |  |
 | + |  | + |
 | график вогнутый | график выпуклый | график вогнутый |
Точек перегиба нет.
8) На основании полученных результатов строим график функции (рис.6)

Рис.6.
171-180. Найти наибольшее и наименьшее значения функции  на отрезке
на отрезке  :
:  ,
,  .
.
Наибольшее и наименьшее значения функции  непрерывной и кусочно-дифференцируемой (дифференцируемой, за исключением, быть может, конечного числа точек) на отрезке
непрерывной и кусочно-дифференцируемой (дифференцируемой, за исключением, быть может, конечного числа точек) на отрезке  достигается или в точках
достигается или в точках  , в которых
, в которых  или
или  не существует, или на концах отрезка.
не существует, или на концах отрезка.
Решение.
1) Находим первую производную функции:



и определяем внутренние критические точки функции  , т.е. точки
, т.е. точки  в которых
в которых  или
или  не существует:
не существует:


 , точек
, точек  в которых
в которых  не существует нет. Таким образом, единственной внутренней критической (стационарной) точкой функции
не существует нет. Таким образом, единственной внутренней критической (стационарной) точкой функции  на отрезке
на отрезке  является точка
является точка  .
.
2) Вычисляем значения функции  во внутренних критических точках и на концах отрезка
во внутренних критических точках и на концах отрезка  :
:  ,
,  ,
,  .
.
3) Сравниваем значения  ,
,  ,
,  и находим наименьшее и наибольшее значения функции
и находим наименьшее и наибольшее значения функции  на отрезке
на отрезке  :
:
 ,
,  .
.
Ответ:  ,
,  .
.
181-190. Составить уравнения касательной и нормали к графику функции  в точке
в точке  :
:  ,
,  .
.
Уравнение касательной к графику функции  в точке
в точке  имеет вид:
имеет вид: 
Уравнение нормали к графику функции  в точке
в точке  имеет вид:
имеет вид:  .
.
Решение.
1) Вычисляем значение функции  в точке
в точке :
:  .
.
2) Находим первую производную функции: 
 и вычисляем её значение в точке
и вычисляем её значение в точке  :
:  .
.
3) Составляем уравнение касательной: 

 и записываем его в виде
и записываем его в виде  :
:  .
.
4) Составляем уравнение нормали: 

 и записываем его в виде
и записываем его в виде  :
:  .
.
Если  , то уравнение нормали записывается в виде:
, то уравнение нормали записывается в виде:  .
.
Ответ:  - уравнение касательной;
- уравнение касательной;  - уравнение нормали.
- уравнение нормали.
191–200. Затраты, необходимые для производства  единиц данной продукции задаётся функцией издержек
единиц данной продукции задаётся функцией издержек  . Продукция реализуется по фиксированной цене
. Продукция реализуется по фиксированной цене  (ден.ед.) за единицу продукции. Требуется найти: а) оптимальное значение
(ден.ед.) за единицу продукции. Требуется найти: а) оптимальное значение  выпуска продукции, при котором производитель получит максимальную прибыль; б) средние значения издержек производства и прибыли при
выпуска продукции, при котором производитель получит максимальную прибыль; б) средние значения издержек производства и прибыли при  ; в) эластичность издержек производства и прибыли при
; в) эластичность издержек производства и прибыли при  . Сделать выводы.
. Сделать выводы.
Прибыль, получаемая производителем при выпуске  единиц данной продукции, задаётся функцией
единиц данной продукции, задаётся функцией  , где
, где  - выручка от реализации
- выручка от реализации  единиц данной продукции по фиксированной цене
единиц данной продукции по фиксированной цене  (ден.ед.) за единицу продукции,
(ден.ед.) за единицу продукции,  - функция издержек.
- функция издержек.
Средними издержками называют величину  (издержки в расчёте на 1 ед. выпускаемой продукции), а средней прибылью – величину
(издержки в расчёте на 1 ед. выпускаемой продукции), а средней прибылью – величину  (прибыль в расчёте на 1 ед. выпускаемой продукции).
(прибыль в расчёте на 1 ед. выпускаемой продукции).
Эластичностью издержек называют величину  (показывает приближённый процентный прирост издержек
(показывает приближённый процентный прирост издержек  при изменении
при изменении  на 1%), а эластичностью прибыли –
на 1%), а эластичностью прибыли –  (показывает приближённый процентный прирост прибыли
(показывает приближённый процентный прирост прибыли  при изменении
при изменении  на 1%).
на 1%).
Решение.
а1) Находим функцию прибыли
 .
.
а2) Находим оптимальное значение  выпуска продукции, при котором производитель получит максимальную прибыль, т.е. находим при каком значении
выпуска продукции, при котором производитель получит максимальную прибыль, т.е. находим при каком значении  выпуска продукции функция прибыли
выпуска продукции функция прибыли  примет наибольшее значение на промежутке
примет наибольшее значение на промежутке  .
.
Если функция одной переменной  на промежутке
на промежутке  имеет единственную точку локального экстремума
имеет единственную точку локального экстремума  , являющуюся точкой локального максимума, то в точке
, являющуюся точкой локального максимума, то в точке  функция принимает своё наибольшее значение на промежутке
функция принимает своё наибольшее значение на промежутке  .
.
Для решения данной задачи находим производную функции  :
:



и определяем её критические точки (точки возможного локального экстремума), принадлежащие промежутку  , т.е. точки в которых
, т.е. точки в которых  или
или  не существует:
не существует: 

 , точек
, точек  в которых
в которых  не существует нет. Таким образом, единственной критической точкой функции
не существует нет. Таким образом, единственной критической точкой функции  на промежутке
на промежутке  является точка
является точка  .
.
Так как  при
при  и
и  при
при  , то точка
, то точка  - является точкой локального максимума и, следовательно, точкой в которой функция
- является точкой локального максимума и, следовательно, точкой в которой функция  на промежутке
на промежутке  принимает наибольшее значение
принимает наибольшее значение  .
.
Итак, оптимальное значение объёма выпускаемой продукции составляет 5 единиц, при этом максимальная прибыль составляет 50 ден.ед.
б) Находим средние издержки производства и среднюю прибыль при  :
: 

 ;
;


 .
.
Итак, в расчёте на единицу выпускаемой продукции издержки производства составляют 90 ден.ед., а прибыль – 10 ден.ед.
в) Находим эластичность издержек производства и прибыли при  :
:




 .
.




 .
.
Итак, при увеличении объёма  выпуска продукции на 1%, издержки производства увеличатся на 1.11%, а прибыль не изменится.
выпуска продукции на 1%, издержки производства увеличатся на 1.11%, а прибыль не изменится.
Ответ: а) ,
,  ; б)
; б) ,
,  ;
;
в) ,
,  .
.