§9. Формула Бернулли
Пусть при проведении некоторого однократного испытания вероятность появления события А равна р, а непоявления –– q = 1 – p. Требуется найти вероятность того, что при n повторных испытаниях событие А произойдет m раз.
Искомую вероятность обозначим Pn(m). Она вычисляется по формуле
Pn(m) = 

Эта формула называется формулой Бернулли. Проиллюстрируем теперь полученную формулу двумя примерами.
Пример 1. Играются шесть партий между двумя шахматистками Аней и Лизой. Считаются только победы и поражения. В случае ничьей, партия не имеет порядкового номера и переигрывается. Вероятность выигрыша каждой отдельной партии Аней равна  . Вероятность выигрыша каждой отдельной партии Лизой равна
. Вероятность выигрыша каждой отдельной партии Лизой равна  . Чему равна вероятность выигрыша всей игры Аней, Лизой и ничейного результата?
. Чему равна вероятность выигрыша всей игры Аней, Лизой и ничейного результата?
Решение. Победит в матче Аня, если она выиграет 4, 5 или 6 партий. Вероятность этого события равна:


Для Лизы вероятность победы в матче равна:


Вероятность ничьей равна:

Пример 2. Вероятность того, что лампа останется неисправной после 1000 ч работы, равна 0,2. Какова вероятность того, что из пяти ламп не менее трех останутся исправными после 1000 ч работы?
Решение. Будем рассматривать горение каждой лампы в течение 1000 ч как отдельный опыт.
Тогда можно сказать, что произведено 5 опытов. Нас интересуют события «горят 3 лампы из 5», «горят 4 лампы из 5», «горят 5 ламп из 5», т.е. мы можем найти вероятность каждого из этих событий по формуле Бернулли, учитывая, что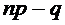 и
и 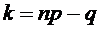 :
: 
Тогда искомая вероятность составит 
Пусть  фиксировано. Тогда
фиксировано. Тогда  превращается в некоторую функцию аргумента k, принимающего значения 0, 1, 2, …,
превращается в некоторую функцию аргумента k, принимающего значения 0, 1, 2, …,  . Выясним при каком значении аргумента эта функция достигает максимума, т.е. какое из чисел
. Выясним при каком значении аргумента эта функция достигает максимума, т.е. какое из чисел  является наибольшим.
является наибольшим.
Составим отношение:

Из неравенств:
а)  откуда
откуда  и
и 
б)  откуда
откуда  и
и  ––
––
следует:
если  , т.е. при увеличении
, т.е. при увеличении  от 0 до
от 0 до  , функция
, функция  возрастает,
возрастает,
при  (если
(если  целое неотрицательное)
целое неотрицательное) 
если  , т.е. при дальнейшем увеличении
, т.е. при дальнейшем увеличении  , функция
, функция  убывает.
убывает.
Целое число  , при котором вероятность
, при котором вероятность  достигает наибольшего значения, называется наивероятнейшим числом успехов.
достигает наибольшего значения, называется наивероятнейшим числом успехов.
Возможны два случая:
а)  –– целое число, тогда целым числом будет и
–– целое число, тогда целым числом будет и  ;
;  ; оба эти числа
; оба эти числа  и
и  равноправно представляют наивероятнейшее число успехов, причем
равноправно представляют наивероятнейшее число успехов, причем
 ;
;
б)  –– нецелое, тогда нецелым числом будет и
–– нецелое, тогда нецелым числом будет и  . Между этими нецелыми числами имеется лишь одно целое значение
. Между этими нецелыми числами имеется лишь одно целое значение  аргумента, большее, чем
аргумента, большее, чем  и меньшее, чем
и меньшее, чем  , т.е. имеется единственное значение
, т.е. имеется единственное значение  , являющееся наивероятнейшим числом успехов; число
, являющееся наивероятнейшим числом успехов; число  есть целый корень двойного неравенства
есть целый корень двойного неравенства
 .
.
Пример 3. При автоматической наводке орудия вероятность попадания по быстро движущейся цели равна 0,9. Найти наивероятнейшее число попаданий при 50 выстрелах.
Решение. Здесь  и
и  ,
,  следовательно,
следовательно,  =45.
=45.
Докажем сейчас, что число  можно рассматривать в определенном смысле как среднее число успехов в
можно рассматривать в определенном смысле как среднее число успехов в  опытах. Условимся называть
опытах. Условимся называть  кратное повторение данного опыта серией. Допустим, что произведено
кратное повторение данного опыта серией. Допустим, что произведено  серий. Пусть в первой серии было получено
серий. Пусть в первой серии было получено  успехов, во второй ––
успехов, во второй ––  ,…, в
,…, в  –й ––
–й ––  . Составим среднее арифметическое этих чисел:
. Составим среднее арифметическое этих чисел:

Записанная выше дробь со знаменателем  есть не что иное, как отношение общего числа успехов в этих
есть не что иное, как отношение общего числа успехов в этих  опытах к числу опытов. С увеличением
опытах к числу опытов. С увеличением  (а значит и
(а значит и  ) эта дробь будет приближаться к числу
) эта дробь будет приближаться к числу  –– вероятности успеха. Таким образом, число
–– вероятности успеха. Таким образом, число  будет приближаться к
будет приближаться к  , что и требовалось получить.
, что и требовалось получить.
Пример 4. В условиях данного предприятия вероятность брака равна 0,03. Чему равно среднее число бракованных изделий на тысячу?
Решение. Искомое число 