Дифференцируемые функции
Рассмотрим функцию 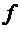 , определенную на промежутке
, определенную на промежутке 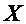 со значениями
со значениями  .
.
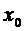 ‑ внутренняя точка промежутка
‑ внутренняя точка промежутка 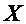 ,
, 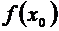 ‑ значение функции
‑ значение функции 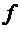 в точке
в точке 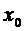 . Возьмем число
. Возьмем число 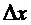 такое, что
такое, что 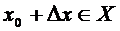 . Величину
. Величину 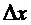 называют приращением аргумента
называют приращением аргумента 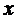 . Величину
. Величину 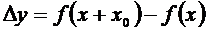 называют приращением функции в точке
называют приращением функции в точке 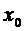 , которое вызвано приращением аргумента
, которое вызвано приращением аргумента 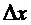 .
. Если для точки 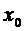 существует число
существует число 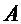 такое, что приращение функции
такое, что приращение функции  представимо в виде:
представимо в виде:
 , , | (1) |
то говорят, что функция  дифференцируема в точке
дифференцируема в точке 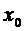 .
.
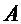 называют производной функции
называют производной функции 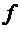 в точке
в точке 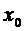 . Из формулы (1) получаем:
. Из формулы (1) получаем:  .
.
Таким образом, дифференцируемость функции в точке 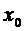 означает, что в этой точке существует производная функции. Производную функции в точке
означает, что в этой точке существует производная функции. Производную функции в точке 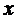 обозначают одним из символов:
обозначают одним из символов:
 и др.
и др.
Отношение  представляет собой среднюю скорость изменения функции
представляет собой среднюю скорость изменения функции 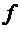 на промежутке с концами
на промежутке с концами 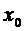 и
и  . Величина
. Величина  ‑ это мгновенная скорость изменения функции
‑ это мгновенная скорость изменения функции 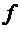 в точке
в точке 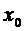 . Например, если
. Например, если 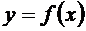 ‑ перемещение точки по оси
‑ перемещение точки по оси  за время
за время 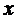 , то
, то 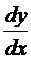 ‑ скорость движения точки. Если функция
‑ скорость движения точки. Если функция 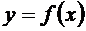 описывает количество продукции, производимой предприятием за время
описывает количество продукции, производимой предприятием за время 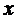 , то
, то  ‑ это средняя производительность за промежуток времени
‑ это средняя производительность за промежуток времени  , а
, а 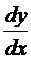 ‑ это производительность в момент времени
‑ это производительность в момент времени 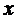 .
.
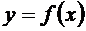 описывает закон изменения капитала в зависимости от времени
описывает закон изменения капитала в зависимости от времени 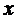 , то
, то 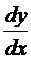 ‑ скорость накопления капитала.
‑ скорость накопления капитала. Итак, если 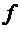 дифференцируема в точке
дифференцируема в точке 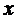 , то
, то
 .
.
Величину  называют дифференциалом функции в точке
называют дифференциалом функции в точке 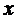 и обозначают обычно символами:
и обозначают обычно символами:
 и др. 1.2 Правила дифференцирования
и др. 1.2 Правила дифференцирования
Будем считать, что функции  дифференцируемы, т.е. имеют производные
дифференцируемы, т.е. имеют производные  . Тогда:
. Тогда:
1°. Функция  дифференцируема и
дифференцируема и  .
.
2°. Если  ‑ постоянная, то функция
‑ постоянная, то функция  дифференцируема и
дифференцируема и  .
.
3°. Из 1° и 2° следует, что  .
.
4°. Функция  дифференцируема и
дифференцируема и  .
.
5°. Из 4° следует, что  .
.
6°. Если  определена и дифференцируема, то
определена и дифференцируема, то  .
.
Основные элементарные функции дифференцируемы всюду, где они определены. Производные этих функций могут быть вычислены по определению, т.е. по формуле:

и с помощью правил дифференцирования.
Полученные значения производных основных элементарных функций приведем в таблице.
 ; ; |  ; ; |
 ; ; |  ; ; |
 |  ; ; |
 ; ; |  ; ; |
 , ,  ; ; |  ; ; |
 ; ; |  ; ; |
 , ,  ; ; |  ; ; |
 ; ; |  . . |
Использование таблицы производных и правил дифференцирования позволяет вычислять производные арифметических комбинаций основных элементарных функций.
Пример 1.  . Вычислить
. Вычислить  .
.

 .
.
Пример 2.  . Вычислить
. Вычислить  .
.


 .
.
Пример 3.  . Вычислить
. Вычислить  .
.
 .
.