1.3. Метод половинного деления
Метод половинного является самым простым и надежным способом решения нелинейного уравнения. Пусть из предварительного анализа известно, что корень уравнения находится на отрезке 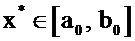 , т.
, т.
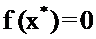 , так, что
, так, что 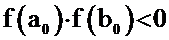 . Пусть функция
. Пусть функция 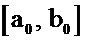 непрерывна на отрезке
непрерывна на отрезке 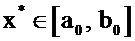 и принимает на концах отрезка значения разных знаков, т.е.
и принимает на концах отрезка значения разных знаков, т.е. 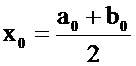 .
. Разделим отрезок 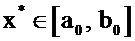 пополам. Получим точку
пополам. Получим точку  . Вычислим значение функции в этой точке:
. Вычислим значение функции в этой точке:  . Если
. Если  , то
, то  – искомый корень, и задача решена. Если
– искомый корень, и задача решена. Если  , то
, то  – число определённого знака:
– число определённого знака:  либо
либо  . Тогда либо на концах отрезка
. Тогда либо на концах отрезка  , либо на концах отрезка
, либо на концах отрезка  значения функции
значения функции 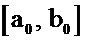 имеют разные знаки. Обозначим такой отрезок
имеют разные знаки. Обозначим такой отрезок 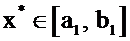 .
.
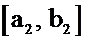 и длина отрезка
и длина отрезка 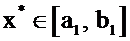 в два раза меньше, чем длина отрезка
в два раза меньше, чем длина отрезка 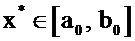 . Поступим аналогично с отрезком
. Поступим аналогично с отрезком 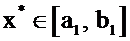 . В результате получим либо корень
. В результате получим либо корень 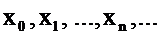 , либо новый отрезок
, либо новый отрезок 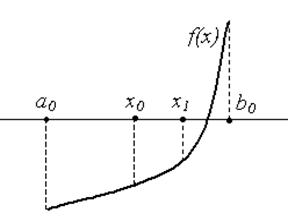 и т. д. (рис. 2).
и т. д. (рис. 2). 
Рис. 2
Середина 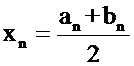 -го отрезка
-го отрезка  . Очевидно, что длина отрезка
. Очевидно, что длина отрезка  будет равна
будет равна  , а так как
, а так как  , то
, то
 . (1)
. (1)
Критерий окончания. Из соотношения (1) следует, что при заданной точности приближения  вычисления заканчиваются, когда будет выполнено неравенство
вычисления заканчиваются, когда будет выполнено неравенство  или неравенство
или неравенство  . Таким образом, количество итераций можно определить заранее. За приближенное значение корня берется величина
. Таким образом, количество итераций можно определить заранее. За приближенное значение корня берется величина  .
.
Пример. Найдем приближенно  с точностью
с точностью  . Эта задача эквивалентна решению уравнения
. Эта задача эквивалентна решению уравнения  , или нахождению нуля функции
, или нахождению нуля функции  .
.
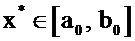 возьмем отрезок
возьмем отрезок 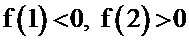 . На концах этого отрезка функция принимает значения с разными знаками:
. На концах этого отрезка функция принимает значения с разными знаками: 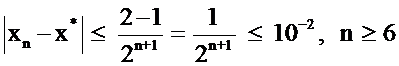 . Найдем число
. Найдем число 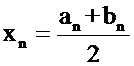 делений отрезка
делений отрезка 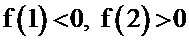 , необходимых для достижения требуемой точности. Имеем:
, необходимых для достижения требуемой точности. Имеем:  .
.
Следовательно, не позднее 6-го деления найдем  с требуемой точностью,
с требуемой точностью,  . Результаты вычислений представлены в таблице 1.
. Результаты вычислений представлены в таблице 1.
Таблица 1
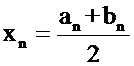 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
 | 1,0000 | 1,0000 | 1,0000 | 1,1250 | 1,1250 | 1,1406 | 1,1406 |
 | 2,0000 | 1,5000 | 1,2500 | 1,2500 | 1,1875 | 1,1875 | 1,1562 |
 | 1,5000 | 1,2500 | 1,1250 | 1,1875 | 1,1406 | 1,1562 | 1,1484 |
Зн  | - | - | - | - | - | - | - |
Зн  | + | + | + | + | + | + | + |
 | 5,5938 | 0,7585 | -0,2959 | 0,1812 | -0,0691 | 0,0532 | -0,0078 |
 – –  | 1,0000 | 0,5000 | 0,2500 | 0,1250 | 0,0625 | 0,0312 | 0,0156 |