Нахождение оптимального управления и оптимальных траекторий без краевых условий. Линия переключения.
Составим сопряженную систему
 .
.
Ее общее решение  т.е.
т.е.
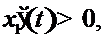 , где
, где 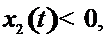 произвольный постоянный вектор.
произвольный постоянный вектор. Составим функцию Понтрягина:
 .
.
Пусть  фиксировано. Если
фиксировано. Если  , то среди всех допустимых значений
, то среди всех допустимых значений  максимальное значение функции Понтрягина доставляет знчение
максимальное значение функции Понтрягина доставляет знчение  . Если
. Если  , то функция
, то функция  получает максимальное значение при
получает максимальное значение при  . Таким образом, при всех
. Таким образом, при всех  (за исключением значения
(за исключением значения  , при котором
, при котором  ) функция управления
) функция управления  , доставляющая максимум функции Понтрягина, принимает только два значения
, доставляющая максимум функции Понтрягина, принимает только два значения  и
и  .
.
Отметим, что условие 2 принципа Понтрягина при таком выборе значений  автоматически выполняется:
автоматически выполняется:

(за исключением одного значения  , при котором
, при котором  ).
).
Согласно принципу максимума Понтрягина, оптимальные траектории можно получить только при значениях  .
.
Пусть  . Тогда система (2) имеет вид
. Тогда система (2) имеет вид  .
.
Ее общее решение
 (3)
(3)
где  произвольные постоянные (их обозначили
произвольные постоянные (их обозначили  в отличие от постоянных
в отличие от постоянных  и
и  в решении сопряженной системы. Кроме того, вместо
в решении сопряженной системы. Кроме того, вместо  записали
записали  , так как
, так как  тоже произвольная постоянная, как и
тоже произвольная постоянная, как и  ). Это – семейство оптимальных фазовых траекторий под управлением
). Это – семейство оптимальных фазовых траекторий под управлением  . Исключая время
. Исключая время  , получим
, получим  семейство парабол.
семейство парабол.
Из уравнения  видно, что с увеличением времени видно, что с увеличением времени  ордината ордината  точки точки  на параболе уменьшается. Следовательно, движение фазовой точки вдоль параболы происходит вниз. на параболе уменьшается. Следовательно, движение фазовой точки вдоль параболы происходит вниз. |  |
Пусть  .
.
 . Её общее решение:
. Её общее решение:  (4)
(4)
Это – семейство оптимальных фазовых траекторий под управлением  . Исключая
. Исключая  , получаем
, получаем  семейство парабол.
семейство парабол.
Из уравнения  видим, что с возрастанием времени видим, что с возрастанием времени  точка точка  движется вдоль параболы вверх. движется вдоль параболы вверх. |  |
Семейства оптимальных траекторий (3) и (4) получены без учета краевых условий. Пока о роли этих семейств можно сказать следующее:
Если точки  и
и  лежат на одной из парабол, то именно кусок этой параболы, соединяющий точки
лежат на одной из парабол, то именно кусок этой параболы, соединяющий точки  и
и  , является оптимальной траекторией (при совпадении направления): объект перейдет из фазового состояния
, является оптимальной траекторией (при совпадении направления): объект перейдет из фазового состояния  в фазовое состояние
в фазовое состояние  за кратчайшее время именно по этой траектории.
за кратчайшее время именно по этой траектории.
Движение фазовой точки  к пункту назначения к пункту назначения  происходит по верхней части параболы семейства (3) при происходит по верхней части параболы семейства (3) при  : : |  |
по нижней части параболы семейства (4) при  :
:
 .
.
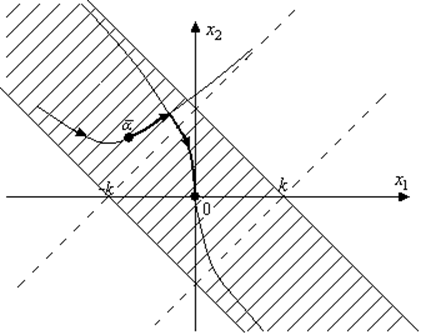
Линия  , составленная из кусков парабол семейств (3) и (4), входящих в начало координат, называется линией переключения.
, составленная из кусков парабол семейств (3) и (4), входящих в начало координат, называется линией переключения.