1.2.6. Теорема (о норме )
Величина, определенная равенством  , является нормой.
, является нормой.
? Докажем для  (для
(для  доказательство аналогично).
доказательство аналогично).
Проверим свойства нормы (1.2.1) учитывая, что для  они проверены.
они проверены.
1) Пусть  , т.е.
, т.е.  . Тогда хотя бы одно из чисел
. Тогда хотя бы одно из чисел  и
и  больше нуля. Если
больше нуля. Если  , то по теореме 1.2.4 (1)
, то по теореме 1.2.4 (1)  . Если
. Если  , то по той же теореме
, то по той же теореме  , т.е.
, т.е.  . Таким образом, в любом случае
. Таким образом, в любом случае  .
.
Пусть обратно,  . Тогда по теореме 1.2.4 (1)
. Тогда по теореме 1.2.4 (1)  , значит,
, значит, 
 .
.
Доказано, что  . Далее
. Далее  очевидно.
очевидно.
2) При  равенство
равенство  очевидно:
очевидно:  и
и  .
.
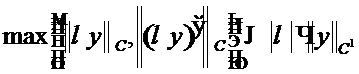 . Тогда то по теореме 1.2.4 (2)
. Тогда то по теореме 1.2.4 (2) 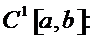 ,
, 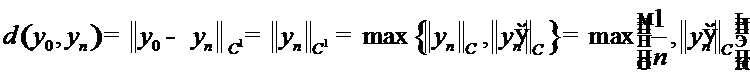 , а согласно замечанию 1.2.5
, а согласно замечанию 1.2.5 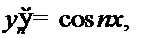 . Поэтому
. Поэтому 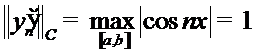 и
и 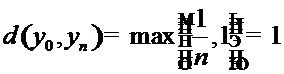 . Значит, и
. Значит, и  , т.е.
, т.е.  . (3)
. (3)
Обратно, 
 по доказанному для
по доказанному для 

 . (4)
. (4)
Из неравенств (3) и (4) получаем  .
.
3) По теореме 1.2.4 (3)  ,
,  , а согласно замечанию 1.2.5
, а согласно замечанию 1.2.5  и
и  . Поэтому
. Поэтому  и
и  , значит,
, значит,  , т.е.
, т.е.
 . ■
. ■
Таким образом, пространство  с нормой
с нормой  является нормированным пространством.
является нормированным пространством.
Расстоянием между точками  является число
является число
 .
.
Замечание. Функции, близкие по норме пространства  , могут сильно отличаться по норме пространства
, могут сильно отличаться по норме пространства  . Например, функции
. Например, функции  и
и  обе принадлежат
обе принадлежат
 | и пространству  и пространству и пространству  (при любых (при любых  (возьмем (возьмем  )). По норме )). По норме  : : |
 . По норме
. По норме 
 .
.
Но 
 , так что
, так что  . С возрастанием
. С возрастанием  функция
функция  становится сколь угодно близкой к функции
становится сколь угодно близкой к функции  по норме
по норме  , т.к.
, т.к.  , тогда как всегда отстоит от неё на расстояние
, тогда как всегда отстоит от неё на расстояние  по норме
по норме  .
.