1.2.3. Теорема (о свойствах расстояния)
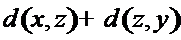 обладает свойствами:
обладает свойствами: 1)  (неотрицательность).
(неотрицательность).
2)  (симметричность),
(симметричность),
3)  (неравенство треугольника).
(неравенство треугольника).
? 1)  (по определению 1.2.1)
(по определению 1.2.1) 
 (по определению 1.2.1).
(по определению 1.2.1).
2)  (по определению 1.2.1)
(по определению 1.2.1) 
 .
.
3)  ( по определению 1.2.1)
( по определению 1.2.1) 
 . ■
. ■
Мы будем иметь дело с множеством функций, непрерывных на отрезке 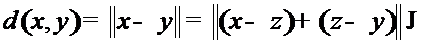 , которое будем обозначать
, которое будем обозначать  , и с множеством функций,
, и с множеством функций,  раз непрерывно дифференцируемых на
раз непрерывно дифференцируемых на 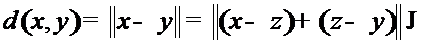 (т.е. имеющих непрерывные производные до
(т.е. имеющих непрерывные производные до  го порядка включительно), которое будем обозначать
го порядка включительно), которое будем обозначать  . Если сложение функций и умножение функции на число понимать как обычно:
. Если сложение функций и умножение функции на число понимать как обычно:
 то при этих линейных операциях множества
то при этих линейных операциях множества  и
и  являются линейными пространствами.
являются линейными пространствами.
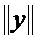 , т.е. имеют непрерывные производные
, т.е. имеют непрерывные производные 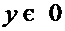 , то сумма
, то сумма 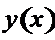 , тоже непрерывно дифференцируема на
, тоже непрерывно дифференцируема на 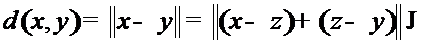 , т.е.
, т.е. 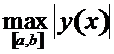 если
если 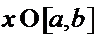 то
то 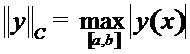 тоже непрерывно дифференцируема на
тоже непрерывно дифференцируема на 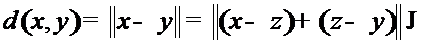 , т.е.
, т.е. 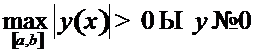 Легко проверить, что эти линейные операции удовлетворяют всем 8 аксиомам линейного пространства, так как при каждом фиксированном
Легко проверить, что эти линейные операции удовлетворяют всем 8 аксиомам линейного пространства, так как при каждом фиксированном 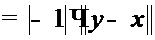 сложение функции и умножение функции на число сводится к сложению и умножению чисел, а для чисел все аксиомы выполняются. Нулевым элементом пространства
сложение функции и умножение функции на число сводится к сложению и умножению чисел, а для чисел все аксиомы выполняются. Нулевым элементом пространства 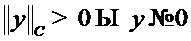 является функция, тождественно равная нулю на
является функция, тождественно равная нулю на 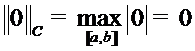 Противоположным элементом для функции
Противоположным элементом для функции 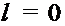 является функция
является функция 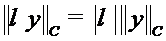 .
. Аналогично,  тоже является линейным пространством.
тоже является линейным пространством.
Итак,  и
и  являются линейными пространствами с обычными правилами сложения функций и умножения функции на число.
являются линейными пространствами с обычными правилами сложения функций и умножения функции на число.
Введем нормы элементов в этих пространствах, что позволит ввести понятие расстояния между элементами этих пространств (т.е.
между функциями). | Норма  есть расстояние от функции есть расстояние от функции  до функции до функции  . В пространстве непрерывных функций . В пространстве непрерывных функций  естественно считать функцию естественно считать функцию  близкой к функции близкой к функции  (на всем отрезке (на всем отрезке |
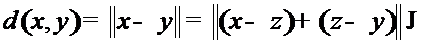 !) если близко к нулю значение
!) если близко к нулю значение  (такое максимальное значение при некотором
(такое максимальное значение при некотором  существует в силу теоремы Вейерштрасса для функции, непрерывной на отрезке).
существует в силу теоремы Вейерштрасса для функции, непрерывной на отрезке).
Поэтому положим  .
.