1.2.11. Теорема (необходимое условие локального экстремума функционала в терминах первой вариации).
Пусть функционал  , определенный на множестве
, определенный на множестве  допустимых вектор–функций
допустимых вектор–функций  с координатами
с координатами  имеет в точке
имеет в точке  локальный экстремум.
локальный экстремум.
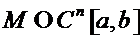 при какой-либо вариации
при какой-либо вариации 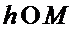 этого аргумента, то эта первая вариация равна нулю:
этого аргумента, то эта первая вариация равна нулю:  .
.
? Пусть, например  точка минимума: существует
точка минимума: существует  такое, что
такое, что

 . Возьмем точку
. Возьмем точку

 . Для нее
. Для нее  . При достаточно малом
. При достаточно малом  будет
будет  , так как
, так как  , где
, где  . Поэтому имеем
. Поэтому имеем

 ,
,
т.е.
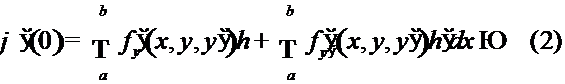
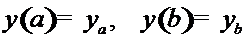 , или
, или 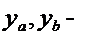 .
. Таким образом, при всех достаточно малых  выполняется неравенство
выполняется неравенство 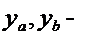 . Это означает, что функция
. Это означает, что функция

имеет минимум в точке  . По условию, при данной вариации
. По условию, при данной вариации 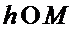 существует первая вариация по аргументу
существует первая вариация по аргументу 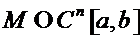 , т.е. существует
, т.е. существует  . Но, по теореме Ферма, если в точке локального экстремума числовая функция числового аргумента имеет производную, то она равна нулю:
. Но, по теореме Ферма, если в точке локального экстремума числовая функция числового аргумента имеет производную, то она равна нулю:  .
.
Следовательно,  . ■
. ■
Замечание. Если найдена вектор – функция  в которой первые вариации функционала
в которой первые вариации функционала  обращаются в нуль, то это ещё не значит, что в точке
обращаются в нуль, то это ещё не значит, что в точке  функционал действительно имеет экстремум: ведь это необходимое условие экстремума. Достаточные условия экстремума функционала сложны, их не будем рассматривать. Но если по смыслу задачи экстремум есть, а найдена только одна вектор – функция
функционал действительно имеет экстремум: ведь это необходимое условие экстремума. Достаточные условия экстремума функционала сложны, их не будем рассматривать. Но если по смыслу задачи экстремум есть, а найдена только одна вектор – функция  , в которой первые вариации обращаются в нуль (“критическая точка”), то в точке
, в которой первые вариации обращаются в нуль (“критическая точка”), то в точке  обязан быть экстремум.
обязан быть экстремум.
В достаточных условиях экстремума используется понятие второй вариации функционала, которое мы не будем рассматривать. Поэтому в дальнейшем вместо “первая вариация” будем говорить просто “вариация”.