1.1.1. Пример.
Построим бесконечно дифференцируемую функцию, положительную на заданном интервале  и равную нулю вне этого интервала.
и равную нулю вне этого интервала.
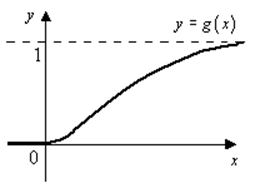
? Покажем сначала, что функция  бесконечно дифференцируема (т.е.
бесконечно дифференцируема (т.е.
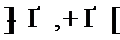 . В точках
. В точках 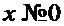 это очевидно: если
это очевидно: если 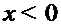 , то
, то 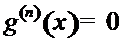 , если
, если 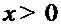 , то
, то 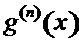 можно найти по правилам дифференцирования. При
можно найти по правилам дифференцирования. При 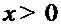 имеем
имеем 

и т.д. Заметим, что производная любого порядка имеет вид
 ,
,
где  некоторый многочлен от
некоторый многочлен от 
 и т.д.
и т.д.
В точке  производные придется вычислять по определению производной:
производные придется вычислять по определению производной:

(если пределы при  слева и справа существуют и совпадают, то их общее значение и будет
слева и справа существуют и совпадают, то их общее значение и будет  ).
).
Ищем 

 так как экспонента растет быстрее
так как экспонента растет быстрее  . Нашли
. Нашли  .
.
Ищем

так как экспонента растет быстрее любого многочлена. Нашли  .
.
Так можно найти  при любом
при любом  : если найдено, что
: если найдено, что  , то
, то


Нашли  .
.
Итак,  бесконечно дифференцируема во всех точках интервала
бесконечно дифференцируема во всех точках интервала 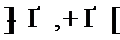 .
.
 |  |  |
Функции 
 тоже бесконечно дифференцируемы во всех точках
тоже бесконечно дифференцируемы во всех точках  как сложные функции, составленные из бесконечно дифференцируемых звеньев (например,
как сложные функции, составленные из бесконечно дифференцируемых звеньев (например,  состоит из бесконечно дифференцируемых функций
состоит из бесконечно дифференцируемых функций  (как было показано) и
(как было показано) и  ).
).

бесконечно дифференцируема на 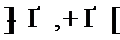 . Это и есть искомая функция. Она положительна на интервале
. Это и есть искомая функция. Она положительна на интервале  , так как
, так как
 |   и равна нулю при и равна нулю при  . . |