Обобщенная теорема Чебышева.
Теорема Чебышева легко может быть обобщена на более сложный случай. Обобщенная теорема Чебышева формулируется следующим образом. Если 
независимые случайные величины с математическими ожиданиями 
и дисперсиями 
и если все дисперсии ограничены сверху одним и тем же числом L:
 |
то при возрастании п среднее арифметическое наблюденных значений величин сходится по вероятности к среднему арифметическому их математических ожиданий.
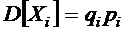— сколь угодно малые положительные числа. Тогда при достаточно большом n  |
Доказательство. Рассмотрим величину
 |
Ее математическое ожидание равно:
 |
а дисперсия
 |
Применим к величине Y неравенство Чебышева:
 |
или
 | (9.2.7) |
Заменим в правой части неравенства (9.2.7) каждую из величин 
большей величиной L. Тогда неравенство только усилится:
 |
Как бы мало ни было 
, можно выбрать п настолько большим, чтобы выполнялось неравенство 
, тогда 
откуда, переходя к противоположному событию, получим доказываемое неравенство.