Лабораторная работа № 2 Конечные цепные дроби.
Рассмотрим рациональное число 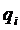 . Будем считать, что
. Будем считать, что  .
.
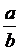 и
и 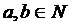 , и выразим
, и выразим 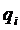 через неполные частные
через неполные частные 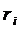 , которые при этом будут получаться. Процесс деления закончиться, поскольку последовательность чисел
, которые при этом будут получаться. Процесс деления закончиться, поскольку последовательность чисел 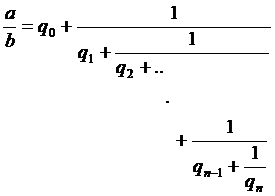 ограничена снизу, где
ограничена снизу, где 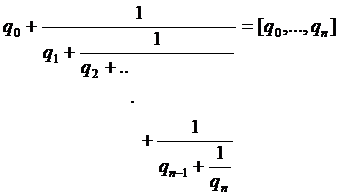 - соответствующие остатки. В итоге получим
- соответствующие остатки. В итоге получим  .
.
Определение 1. Выражение вида  называется конечной цепной (непрерывной) дробью длины
называется конечной цепной (непрерывной) дробью длины  .
.
Теорема 1. Всякое рациональное число может быть представлено в виде конечной цепной дроби.
Пример 1. Дана конечная цепная дробь вида [3,2,4,5,2]. Найти рациональное число, соответствующее этой дроби.
Решение:

Пример 2. Разложить в непрерывную дробь  .
.
Решение:
 =
= .
.
Определение 2. Подходящей дробью порядка  ,
,  к данной цепной дроби
к данной цепной дроби  называется цепная дробь
называется цепная дробь  и обозначается через
и обозначается через  .
.
Как видно из определения значение подходящей дроби любого порядка нетрудно получить простым свертыванием ее в обыкновенную дробь, однако, данный процесс при больших  оказывается весьма громоздким. Свойства подходящих дробей позволяют рационализировать этот процесс.
оказывается весьма громоздким. Свойства подходящих дробей позволяют рационализировать этот процесс.
Теорема 2. Числитель и знаменатель подходящей дроби  -ого порядка
-ого порядка  выражаются через числители и знаменатели двух предыдущих подходящих дробей по следующим формулам:
выражаются через числители и знаменатели двух предыдущих подходящих дробей по следующим формулам:


Данная формула справедлива для  , но если условно ввести
, но если условно ввести  , то ею можно пользоваться при любых
, то ею можно пользоваться при любых  . При этом вычисления удобно записывать в таблице.
. При этом вычисления удобно записывать в таблице.
Пример 3. Вычислить все подходящие дроби к дроби  .
.
Решение.
 =[1,2,1,2,4].
=[1,2,1,2,4].
 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
 | 1 | 2 | 1 | 2 | 4 | ||
 | 0 | 1 | 1 | 3 | 4 | 11 | 48 |
 | 1 | 0 | 1 | 2 | 3 | 8 | 35 |
Таким образом 
Задания для самостоятельной работы.
1. Разложить в непрерывную дробь 
2. Свернуть непрерывные дроби [1,1,2,1,2,1,2]; [0,1,2,3,4,5]; [5,4,3,2,1]; [a,b,a,b,a]
3. Разложить в непрерывную дробь  и составить таблицу подходящих дробей.
и составить таблицу подходящих дробей.
4. Сократить при помощи разложения в цепную дробь 1)  .
.
5. Доказать несократимость дроби  .
.
6. Заменить подходящей дробью третьего порядка и оценить погрешность 
7. Применить соотношение  к решению в целых числах уравнения
к решению в целых числах уравнения  .
.
8. Решить найденным способом уравнение 
9. Решить уравнения 1)  .
.