Лабораторная работа № 3 Бесконечные цепные дроби.
Определение 1. Иррациональность называется квадратичной, если она удовлетворяет квадратному уравнению с рациональными коэффициентами.
Общий вид квадратичной иррациональности:  ,
,  .
.
Определение 2. Выражение вида  называется бесконечной цепной дробью.
называется бесконечной цепной дробью.
Определение 3. Если в бесконечной цепной дроби значения неполных частных, начиная с некоторого момента, повторяются, то дробь называется бесконечной периодической цепной дробью, причем чисто периодической, если повторения начинаются с нулевого звена и смешанно-периодической в противном случае.
Теорема. Квадратичные и только квадратичные иррациональности разлагаются в периодическую непрерывную дробь.
Пример 1. Разложить в периодическую непрерывную дробь  .
.
Решение. Имеем  (целая часть),
(целая часть),  (дробная часть).
(дробная часть).
Рассмотрим  . Таким образом
. Таким образом  . Так как
. Так как  , следовательно
, следовательно  . В итоге получим
. В итоге получим  .
.
Пример 2. Найти величину дроби [3,(1,1,1,1,6)].
Решение. Пусть  .
.
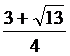 . Найдем
. Найдем 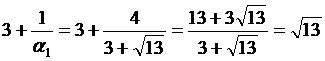 . Составим таблицу подходящих дробей:
. Составим таблицу подходящих дробей:  | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
 | 1 | 1 | 1 | 1 | 6 | 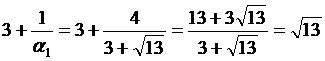 | ||
 | 0 | 1 | 1 | 2 | 3 | 5 | 33 |  |
 | 1 | 0 | 1 | 1 | 2 | 3 | 20 |  |
Имеем  . Решая данное уравнение, получим корни
. Решая данное уравнение, получим корни  , из которых выбираем положительный
, из которых выбираем положительный  .
.
Таким образом, искомое число равно  .
.
Задания для самостоятельной работы.
1. Свернуть непрерывные периодические дроби 1)  .
.
2. Найти иррациональность  , если
, если  .
.
3. Разложить в непрерывную дробь 1)  .
.
4. Разложить в непрерывную дробь  .
.