1.4. Выборочное уравнение прямой линии регрессии по сгруппированным данным. Выборочный коэффициент корреляции
Для отыскания параметров прямой линии регрессии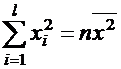 
по несгруппированным данным по методу наименьших квадратов получена система:
(1)
где 
– коэффициент регрессии.
Пусть получено большое число данных (для удовлетворительной оценки искомых параметров количество наблюдений должно быть не менее 50). Среди них есть повторяющиеся, и они сгруппированы в виде корреляционной таблицы. Запишем соотношение (1) так, чтобы оно отражало данные корреляционной таблицы.
; 
; 
; 
; 
;
; 
.
Учтено, что пара чисел наблюдалась 
раз. Поставив все это в систему (1) будем иметь
(2)
Решив эту систему, найдем параметры и 
и тем самым найдем уравнение регрессии .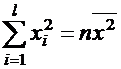
Однако целесообразно, введя новую величину – коэффициент корреляции, найти уравнение регрессии в ином виде.
Из 2-го уравнения системы выразим : 
.
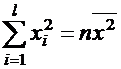получим 
;
. (3)
Найдем из системы (2) коэффициент корреляции 
:
, (4)
где 
– среднее квадратическое отклонение СВ 
.
Умножая обе части равенства на дробь 
, получим выборочный коэффициент корреляции
(5)
Выборочный коэффициент корреляции служит для оценки тесноты линейной корреляционной зависимости.
Отсюда выборочное уравнение прямой линии регрессии 
на имеет вид
. (6)
Аналогично находят второе уравнение прямой линии регрессии
. (7)