1.5. Свойства выборочного коэффициента корреляции
1. Абсолютная величина выборочного коэффициента корреляции не превосходит 1 (
).
2. Если выборочный коэффициент корреляции равен 0 и выборочные линии регрессии – прямые линии, то 
и 
не связаны линейной корреляционной зависимостью и 
, 
.
В этом случае прямые линии регрессии параллельны соответственно координатным осям.
Замечание. Если выборочный коэффициент корреляции 
, то признаки и могут быть связаны нелинейной корреляционной или даже функциональной зависимостью.
3. Если абсолютная величина 
, то наблюдаемые значения признаков связаны линейной функциональной зависимостью.
4. С возрастанием абсолютной величины выборочного коэффициента корреляции линейная корреляционная зависимость становится более тесной и при переходит в функциональную.
Величина коэффициента корреляции характеризует силу линейной связи между признаками ():
если 
– связь слабая;
если 
– связь умеренная;
если 
– связь заметная;
если 
– связь высокая;
если 
– связь весьма высокая;
если – связь функциональная.
5.
Знак выборочного коэффициента корреляции совпадает со знаком выборочного коэффициента регрессии: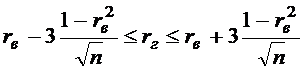
, 
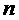и определяет направление связи. Если 
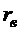– связь прямая, 
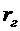– связь обратная. Перемножим первое и второе равенства 
; 
.
Знак при радикале должен совпадать со знаком коэффициента регрессии, т.е. 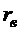, если 
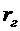; , если 
.
Выборочный коэффициент корреляции равен среднему геометрическому выборочных коэффициентов регрессий.