1. Основные понятия и задачи
Теория вероятностей и математическая статистика, как и другие разделы математики, изучают явления окружающего мира не непосредственно, а с помощью математических моделей.
Во многих случаях требуется установить и оценить зависимость случайной величины (СВ)  от одной или нескольких СВ.
от одной или нескольких СВ.
При функциональной связи каждому значению одной величины (аргумента) соответствует одно значение другой величины (функции).
Как бы точно не проводился эксперимент, как бы точно не закреплялись условия опыта и побочные факторы, неизбежен некоторый разброс результатов опыта в силу того, что не учтены действия еще многих факторов, то есть между изучаемыми величинами если и есть какая либо связь, то явно не функциональная.
Строгая функциональная зависимость реализуется редко, так как обе величины или одна из них подвержены еще действию случайных факторов, причем среди них могут быть общие для обеих величин (под общими здесь понимают факторы, при которых возникает статистическая зависимость).
Статистической называют зависимость, при которой изменение значения одной из величин влечет за собой изменение значения другой величины. В частности, статистическая зависимость проявляется в том, что при изменении одной величины изменяется среднее значение другой величины. В этом случае статистическую зависимость называют корреляционной.
Введем понятие условной средней.
Определение. Условной средней  называют среднее арифметическое значений
называют среднее арифметическое значений  , соответствующих значению
, соответствующих значению  .
.
Если каждому значению  соответствует одно значение условной средней, то условная средняя есть функция от
соответствует одно значение условной средней, то условная средняя есть функция от  . В этом случае говорят, что случайная величина
. В этом случае говорят, что случайная величина  зависит от
зависит от 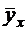 корреляционно.
корреляционно.
Определение. Корреляционной зависимостью  от
от 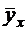 называется функциональную зависимость условной средней
называется функциональную зависимость условной средней  от
от  , то есть
, то есть  . Это уравнение регрессии
. Это уравнение регрессии  на
на 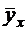 . Функцию
. Функцию  называют регрессией
называют регрессией  на
на 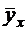 , а ее график – линией регрессии
, а ее график – линией регрессии  на
на 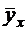 .
.
Определение. Условной средней  называют среднее арифметическое значений X, соответствующих значению
называют среднее арифметическое значений X, соответствующих значению  .
.
Определение. Корреляционной зависимостью 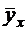 от
от  называют функциональную зависимость условной средней
называют функциональную зависимость условной средней  от
от  , то есть
, то есть  .
.
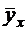 на
на  . Функцию
. Функцию 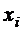 называют регрессией
называют регрессией 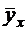 на
на  , а ее график – линией регрессии
, а ее график – линией регрессии 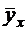 на
на  .
.