§ 9. Сходимость по распределению.
9.1. Пусть на (Ω,F,P) задана последовательность 
случайных элементов со значениями в 
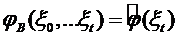, где E - польское пространство, т.е.
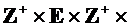алгебра на E. Определение. Будем говорить, что - последовательность случайных элементов 
со значениями в E сходится по распределению при 
к случайному элементу 
со значениями в E и обозначать 
, если для любой функции 
Сb(E), где Сb(E) - пространство непрерывных ограниченных на E функций со значениями в R1, справедливо 
() = M().
Определение. Семейство вероятностных мер 
на на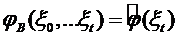зывается слабо сходящимся к некоторой мере P0 и обозначается Pn 
P0 , если для любой Сb(E)
= 
.
Из этих определений вытекает утверждение.
Теорема 35. Пусть 
- семейство случайных элементов, а 
соответствующее им семейство распределений 
, тогда и только тогда, когда Pn 
Pо , т.е. () = M(
), для 
Сb(E).
9.2.
Определение. Семейство вероятностных мер {Pn}n>1 на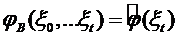 называется относительно компактным, если оно содержит подпоследовательность, слабо сходящуюся к некоторой вероятностной мере Р. Определение. Семейство вероятностных мер {Pn}n>1 называется плотным, если для любого 
>0 существует компакт 
E такой, что 
Рn(
< 
.
Приведем достаточное условие плотности семейства {Pn}n>1.
Предложение 36. Если последовательность случайных величин 
, где 
>0, равномерно интегрируема, то семейство {Pn}n>1 плотно.
9.3. Следующее утверждение играет фундаментальную роль в теории слабой сходимости.
Теорема 37 (Прохоров) Пусть {Pn}n>1 – семейство вероятностных мер на . {Pn}n>1 – относительно компактно тогда и только тогда, когда оно является плотным. (без доказательства).
9.4. Теорема 38. Справедливы следующие импликации:
1) 
, 2) 
,
3) 
.
Доказательство этого утверждения можно найти например в [ 1 ].