§7 Процессы с независимыми приращениями.
7.1. Пусть E - линейное пространство, а  -s-алгебра борелевских множеств на нем. Через
-s-алгебра борелевских множеств на нем. Через , где
, где , обозначим "параллельный" сдвиг множества B на вектор x, точнее:
, обозначим "параллельный" сдвиг множества B на вектор x, точнее:  .
.
Пусть  семейство вероятностных мер на
семейство вероятностных мер на  удовлетворяющих условиям:
удовлетворяющих условиям:
i)  -
-  -измеримая функция по x для
-измеримая функция по x для  ;
;
ii) если  , то справедливо равенство
, то справедливо равенство
 (38)
(38)
Очевидно следующее равенство
 (39)
(39)
Действительно. Если  , то равенство (39) очевидно. Стало быть, (39) справедливо для простых функций, поэтому, в силу теоремы о монотонной сходимости, равенство (39) остается справедливым для любой измеримой ограниченной функции. Из (38) следует равенство
, то равенство (39) очевидно. Стало быть, (39) справедливо для простых функций, поэтому, в силу теоремы о монотонной сходимости, равенство (39) остается справедливым для любой измеримой ограниченной функции. Из (38) следует равенство
 (40)
(40)
Из (39) следует, что если положить  , то
, то  - будет вероятностью перехода, которая обладает свойством пространственной однородности, т.е. для
- будет вероятностью перехода, которая обладает свойством пространственной однородности, т.е. для  Очевидно, что верно обратное утверждение, если переходная вероятность обладает свойством пространственной однородности, то
Очевидно, что верно обратное утверждение, если переходная вероятность обладает свойством пространственной однородности, то 
7.2.
Пусть q- вероятностная мера на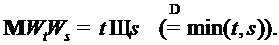 и
и 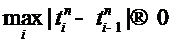 , где
, где 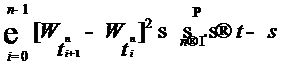 - вероятностная мера на
- вероятностная мера на 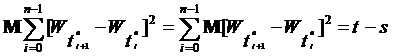 , определенная формулой
, определенная формулой  (41)
(41)
причем  где
где  - переходная вероятность.
- переходная вероятность.
Определение. МПШ  со значениями в линейном измеримом пространстве (E,E) называется процессом с независимыми приращениями, если для
со значениями в линейном измеримом пространстве (E,E) называется процессом с независимыми приращениями, если для  N
N , tk Î R+,
, tk Î R+,  t1
t1