§ 1 Основные определения.
1.1. Пусть  – измеримое пространство, кроме того, положим, что на
– измеримое пространство, кроме того, положим, что на 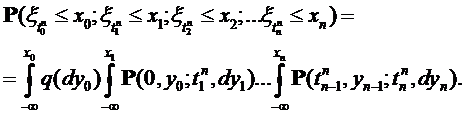 выделено семейство
выделено семейство 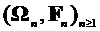 алгебр {Fn}n>0 , обладающих свойствами:
алгебр {Fn}n>0 , обладающих свойствами:
а) для любого 

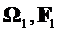 ;
;
б)  для любых
для любых  и
и  ;
;
в) 
Определение.
Семейство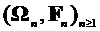 алгебр
алгебр 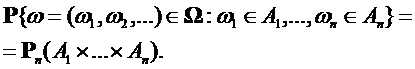 на
на 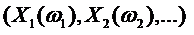 , обладающих свойствами а), б), в) будем называть потоком
, обладающих свойствами а), б), в) будем называть потоком 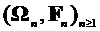 алгебр или фильтрацией. Измеримое пространство (
алгебр или фильтрацией. Измеримое пространство ( ,
,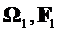 ) с выделенной фильтрацией
) с выделенной фильтрацией 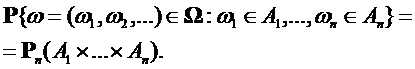 будем называть фильтрованным измеримым пространством и обозначать через (
будем называть фильтрованным измеримым пространством и обозначать через (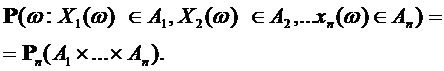 ,
,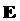 ,
,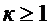 ).
). Определение. Фильтрованным вероятностным пространством или стохастическим базисом называется четверка (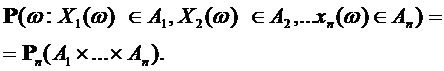 ,
,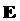 ,
,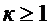 , Р), где Р – вероятностная мера на фильтрованном измеримом пространстве, причем
, Р), где Р – вероятностная мера на фильтрованном измеримом пространстве, причем  – пополнена множествами нулевой меры Р.
– пополнена множествами нулевой меры Р.
Замечание. Напомним,  – пополнена множествами нулевой меры Р. Пусть любой элемент В
– пополнена множествами нулевой меры Р. Пусть любой элемент В , Np
, Np  {A
{A  F: P(A) = 0} и к В добавим Np, т.е.
F: P(A) = 0} и к В добавим Np, т.е.  . С помощью множеств
. С помощью множеств  построим новую
построим новую 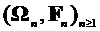 алгебру, обозначаемую
алгебру, обозначаемую  . Ясно, что
. Ясно, что  содержит
содержит  -
- 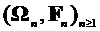 алгебра, её называют пополнением
алгебра, её называют пополнением  относительно меры Р.
относительно меры Р.
Определение. Будем говорить, что последовательность { со значениями в измеримом пространстве
со значениями в измеримом пространстве  согласована с фильтрацией
согласована с фильтрацией 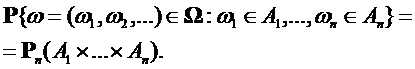 , если при каждом n она
, если при каждом n она 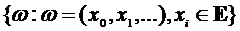 - измерима , т.е.
- измерима , т.е.
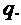
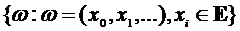 для любого В
для любого В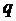 E, и для нее будем использовать обозначение (
E, и для нее будем использовать обозначение (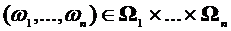 ,
,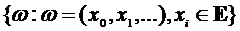 )n>1.
)n>1. 1.2. Пусть на стохастическом базисе (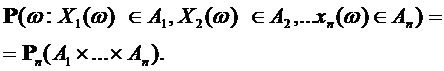 ,
,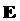 ,
,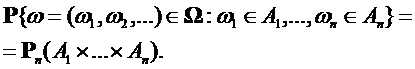 ,Р) задана согласованная последовательность {
,Р) задана согласованная последовательность { . Введем обозначения: а) F
. Введем обозначения: а) F =
=  алгебру, порожденную
алгебру, порожденную  , б) F
, б) F =
= , в)
, в)  =
= эту
эту 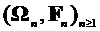 алгебру называют обычно хвостовой.Очевидно, что
алгебру называют обычно хвостовой.Очевидно, что 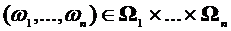 -
-  - измерима.
- измерима.
1.3. Определение. Последовательность (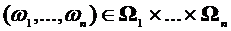 ,
, )n>0 называется марковской, если Р - п.
)n>0 называется марковской, если Р - п.
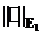
Р(В| ) = P(B|
) = P(B| ), (1)
), (1)
где 
 .
.
1.3.1 Замечание. В силу теоремы 11 главы 1 (теоремы Бореля) существуют для 
 борелевские функции
борелевские функции  , где
, где  и
и  такие, что Р - п. н. Р(В|
такие, что Р - п. н. Р(В| ) =
) =  , P(B|
, P(B| ) =
) =  . Поэтому (1) можно переписать в виде Р - п. н.
. Поэтому (1) можно переписать в виде Р - п. н.
 .
.
1.4. Определение. Пусть Р: 
 , обозначаемая через P(s,
, обозначаемая через P(s, ,t,B), s0 ,если Р(s,
,t,B), s0 ,если Р(s, ,t,B)
,t,B) = P
= P
 ) Р - п.
) Р - п.
Теорема 1 (Чепмен-Колмогоров). Пусть ( ,
, )t>0 – марковская последовательность, а {Р(s,
)t>0 – марковская последовательность, а {Р(s, ,t,B)} – соответствующее ей семейство переходных вероятностей. Тогда для любых
,t,B)} – соответствующее ей семейство переходных вероятностей. Тогда для любых  справедливо равенство
справедливо равенство
Р(s, ,t,B) =
,t,B) =  . (2)
. (2)
Доказательство. Пусть  , тогда Р -п.н. Р(s,
, тогда Р -п.н. Р(s, ,t,B) = P
,t,B) = P
 ) = P(
) = P(
 ) = M(
) = M(
 )=M[M(
)=M[M(
 )|
)| ]=M[P(
]=M[P(
 )|
)| ]= =M[P
]= =M[P F
F ]=
]=
 )P
)P

Доказательство закончено.