§2. Описание простейшей системы массового обслуживания.
2.1. Пусть на стохастическом базисе  заданы 2 точечных процесса
заданы 2 точечных процесса  , i=1,2, и неотрицательная, интегрируемая,
, i=1,2, и неотрицательная, интегрируемая,  - измеримая случайная величина
- измеримая случайная величина  .
.
Определение. Точечный процесс  будем называть входным потоком.
будем называть входным потоком.
Определение. Случайную величину  - измеримую будем называть внутренним состоянием или начальной очередью.
- измеримую будем называть внутренним состоянием или начальной очередью.
Определение. Пусть  , а
, а  . Процесс
. Процесс  назовём простым процессом обслуживания или очередью.
назовём простым процессом обслуживания или очередью.
2.2. Теорема 7. Пусть  – простой процесс обслуживания. Тогда он допускает представление P –п. н.
– простой процесс обслуживания. Тогда он допускает представление P –п. н.
 . (4)
. (4)
Доказательство. Момент времени  является моментом скачка вниз процесса
является моментом скачка вниз процесса  если и только если выполняются условия: а)
если и только если выполняются условия: а)  ,
,
б)  .
.
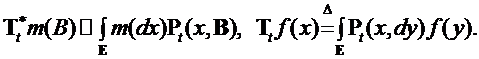 - п. н.
- п. н.  . (5)
. (5)
Так как  , то из (5) следует, что P - п. н.
, то из (5) следует, что P - п. н.
 . (6)
. (6)
Из (6) следует, что P - п. н.
 . (7)
. (7)
Очевидно, что  P - п. н. для любого
P - п. н. для любого  , поэтому
, поэтому  P - п. н. для любого
P - п. н. для любого  . Из определения процесса
. Из определения процесса  следует, что для любого
следует, что для любого  P - п. н., в силу (7),
P - п. н., в силу (7),


Отсюда следует утверждение теоремы.
2.3. Из теоремы 7 вытекает определение.
Определение. Точечный процесс  , определяемый равенством
, определяемый равенством  , называется выходным потоком.
, называется выходным потоком.
2.4. Установим условия, при которых уравнение (4) разрешимо. Для этих целей нам понадобится ряд определений. Без ограничения общности можно считать, что  .
.
Определение. Будем говорить, что (4) имеет сильное решение, если для любого 
 - измеримо, Р - п.
- измеримо, Р - п.
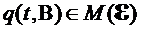 и обращает (4) в тождество.
и обращает (4) в тождество. Определение. Пусть  – два решения уравнения (4), причём
– два решения уравнения (4), причём  . Будем говорить, что (4) имеет единственное сильное решение, если
. Будем говорить, что (4) имеет единственное сильное решение, если  Р - п. н., где
Р - п. н., где  .
.
Теорема 8.Уравнение (4) имеет единственное решение.
Доказательство. Из уравнения (4) следует, что для любого  Р - п. н.
Р - п. н.
 .
.
Отсюда следует, что  Р - п. н. для любого
Р - п. н. для любого  .
.
Заметим, что если решение уравнения (4) существует, то оно имеет кусочно-постоянную траекторию. Поэтому доказательство того факта,
что  - измеримо проведём по индукции. Пусть
- измеримо проведём по индукции. Пусть  - измеримо. Покажем, что
- измеримо. Покажем, что  - измеримо, где
- измеримо, где  и
и  – марковские моменты, которые нагружают простой процесс обслуживания. Из (4) следует, что при
– марковские моменты, которые нагружают простой процесс обслуживания. Из (4) следует, что при  Р - п. н. Поэтому при
Р - п. н. Поэтому при  Р - п.
Р - п.
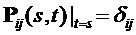 .
. Из последнего равенства следует, что  - измеримо. Таким образом, основной шаг индукции обоснован, а вместе с ним установлено существование решения уравнения (4).
- измеримо. Таким образом, основной шаг индукции обоснован, а вместе с ним установлено существование решения уравнения (4).
Перейдём теперь к доказательству единственности решения (4). Его мы также проведём по индукции. Пусть  – два решения уравнения (4), причём
– два решения уравнения (4), причём  . Так как
. Так как  имеет кусочно-постоянные траектории, то Р - п. н. для
имеет кусочно-постоянные траектории, то Р - п. н. для 
 . (8)
. (8)
Рассмотрим разность  . Пусть
. Пусть  Р - п. н. Покажем, что
Р - п. н. Покажем, что  Р - п. н. Из (8) следует, что Р - п. н.
Р - п. н. Из (8) следует, что Р - п. н.  .
.
Отсюда следует, что основной шаг индукции доказан, а вместе с ним и утверждение теоремы.
2.5. Комментарии. 1) Из выведенного нами уравнения (4) для простого процесса обслуживания следует описание функционирования системы массового обслуживания (однолинейной). Представим себе, что имеется некоторый поток заявок  , поступающий на вход системы, которая представляет собой накопитель заявок и прибор, обслуживающий эти заявки. При этом полагаем, что: а) если прибор обслуживает некоторую заявку, то из накопителя заявки не могут поступить на обслуживающий их прибор; б) если заявка обслужилась прибором, то в прибор поступает следующая заявка и т.д.; в) время, в течение которого заявка обслуживается, определяется как
, поступающий на вход системы, которая представляет собой накопитель заявок и прибор, обслуживающий эти заявки. При этом полагаем, что: а) если прибор обслуживает некоторую заявку, то из накопителя заявки не могут поступить на обслуживающий их прибор; б) если заявка обслужилась прибором, то в прибор поступает следующая заявка и т.д.; в) время, в течение которого заявка обслуживается, определяется как  , где
, где  – последовательность марковских моментов, которая погружает точечный процесс
– последовательность марковских моментов, которая погружает точечный процесс  , г) после того, как заявка обслужилась, она покидает систему.
, г) после того, как заявка обслужилась, она покидает систему.
 |
Рис. 1.
( - накопитель,
- накопитель,  - начальная очередь).
- начальная очередь).
2) Основными задачами теории массового обслуживания являются:
а) математическое описание процессов обслуживания  , который указывает, какое количество заявок находится в данный момент времени в системе, т.е. какова длина очереди; б) нахождение распределения вероятностей длины очереди в системе массового обслуживания и ряда других функционалов, заданных траекториях процесса обслуживания.
, который указывает, какое количество заявок находится в данный момент времени в системе, т.е. какова длина очереди; б) нахождение распределения вероятностей длины очереди в системе массового обслуживания и ряда других функционалов, заданных траекториях процесса обслуживания.
2.6. Выведем теперь уравнения, описывающие эволюцию во времени распределения вероятностей длины очереди.
Теорема 9. Пусть для любого  Р - п. н. Пусть
Р - п. н. Пусть  и
и  измеримы интенсивности точечных процессов
измеримы интенсивности точечных процессов  и
и  , а
, а  ,
,
 . Тогда для любого
. Тогда для любого 
 (9)
(9)
Доказательство. Рассмотрим  .
.
 (10)
(10)
Заметим теперь, что:
i)  . (11)
. (11)
ii)  (12)
(12)
Поэтому (10) с учетом (11) и (12) можно переписать в виде:
 (13)
(13)
Возьмем математическое ожидание относительно левой и правой частей равенства (13). Учитывая, что:
i)  ,
,
ii)  ,
,
Имеем 
 .
.
В силу теоремы Фубини и того, что мера Лебега одноточечных множеств равна нулю, последнее равенство можно переписать в виде:
 (14)
(14)
Заметим теперь, что для любого  имеем:
имеем:
i)  (15)
(15)
 ,
,
ii) 
 . (16)
. (16)
Поэтому (14) с учетом (15), (16) будет иметь вид (9). Доказательство закончено.
2.7. Следствие 10. Пусть выполнены условия теоремы 9. Тогда для любых  и почти всех t существует производная
и почти всех t существует производная  и
и  , удовлетворяет уравнению Колмогорова:
, удовлетворяет уравнению Колмогорова:
 (17)
(17)
Доказательство. Из доказательства теоремы 9 следует, что для любого 
 абсолютно непрерывнa относительно меры Лебега. Отсюда, в силу теоремы Радона – Никодима, существует плотность
абсолютно непрерывнa относительно меры Лебега. Отсюда, в силу теоремы Радона – Никодима, существует плотность  для почти всех t. Отсюда следует утверждение следствия.
для почти всех t. Отсюда следует утверждение следствия.
2.8. Приведем теперь условия, выполнение которых обеспечивает разре-шимость бесконечной системы уравнений (17).
Теорема 11. Пусть выполняются условия:
i)  для любого n и t;
для любого n и t;
ii)  .
.
Тогда в классе  существует единственное решение уравнения (9). Доказательство. Отметим, что если выполнены условия i),ii), то выполнены условия теоремы 30 главы 3. Поэтому разрешимость этого уравнения следует из теоремы 30 главы 3.
существует единственное решение уравнения (9). Доказательство. Отметим, что если выполнены условия i),ii), то выполнены условия теоремы 30 главы 3. Поэтому разрешимость этого уравнения следует из теоремы 30 главы 3.
Замечания. 1) Процесс  со значениями в
со значениями в  , эволюция распределения вероятностей которого описывается уравнением (9), называют обычно процессом гибели-размножения, если
, эволюция распределения вероятностей которого описывается уравнением (9), называют обычно процессом гибели-размножения, если  не зависят от
не зависят от  для любого
для любого  .
.
2) Из доказательства теоремы 11 следует, что бесконечная система уравнений (17) является частным случаем системы уравнений Колмогорова, соответствующей марковским процессам с конечным или счетным числом состояний.
3) Систему уравнений (17) можно переписать в другом виде:
 (18)
(18)
которая с точки зрения теории дифференциальных уравнений представляет собой бесконечную систему дифференциально-разностных уравнений с граничным условием (18), решение которого допускает вероятностную интерпретацию:  .
.
§3. Простейшие системы массового обслуживания с обратной связью.
3.1. В данном пункте мы дадим описание простейшей системы массового обслуживания с обратной связью.
Пусть на стохастическом базисе  заданы два точечных процесса
заданы два точечных процесса  , с
, с  - измеримыми интенсивностями
- измеримыми интенсивностями  , соответственно, кроме того, на нем задана последовательность бернулли-евских случайных величин
, соответственно, кроме того, на нем задана последовательность бернулли-евских случайных величин  , принимающая значения {0,1}, причем
, принимающая значения {0,1}, причем  . Предположим, что
. Предположим, что  - последовательность марковских моментов, которые нагружают точечный процесс
- последовательность марковских моментов, которые нагружают точечный процесс  . Обозначим
. Обозначим  опциональный случайный процесс с кусочно-постоянными траекториями:
опциональный случайный процесс с кусочно-постоянными траекториями:

Осуществим прореживание точечного процесса  с помощью последовательности
с помощью последовательности  :
:

Как и в §1, введем процессы 
 .
.
Очевидно, что  Р – п. н. для любого
Р – п. н. для любого  . Теперь определим простой процесс обслуживания
. Теперь определим простой процесс обслуживания  и назовем его процессом обслуживания для системы с обратной связью. Ясно, что:
и назовем его процессом обслуживания для системы с обратной связью. Ясно, что:

Обозначим

и назовем его процессом (потоком) обратной связи.
Через  обозначим процесс:
обозначим процесс:
 (20) Положим
(20) Положим  . Очевидно, что из приведенных построений следует, что
. Очевидно, что из приведенных построений следует, что  (21) для любого момента времени t и
(21) для любого момента времени t и  , (22)
, (22)
где  - выходной поток.
- выходной поток.
3.2. Комментарий. Выше приведенное построение процесса  имеет простую интерпретацию: на вход системы массового обслуживания (СМО) поступает поток заявок
имеет простую интерпретацию: на вход системы массового обслуживания (СМО) поступает поток заявок . Затем, поток обслуженных заявок
. Затем, поток обслуженных заявок  прореживается последовательностью
прореживается последовательностью  по следующему правилу: если
по следующему правилу: если  , то она поступает на вход системы массового обслуживания в накопитель необслуженных заявок, т.е. должна быть обслужена снова, последнее означает, что обслуживание произведено некачественно (брак); если
, то она поступает на вход системы массового обслуживания в накопитель необслуженных заявок, т.е. должна быть обслужена снова, последнее означает, что обслуживание произведено некачественно (брак); если  , то заявка обслужена качественно (не брак) и она покидает систему массового обслуживания. Ниже на рис. 2 приведена структурная схема СМО с обратной связью.
, то заявка обслужена качественно (не брак) и она покидает систему массового обслуживания. Ниже на рис. 2 приведена структурная схема СМО с обратной связью.
 |
Рис. 2.
3.3. Для описанных выше систем массового обслуживания справедливы следующие утверждения.
Теорема 12. Пусть  – простой процесс обслуживания с обратной связью. Тогда для любого
– простой процесс обслуживания с обратной связью. Тогда для любого  Р - п. н. допускает представление:
Р - п. н. допускает представление:
1)  , где
, где  и
и  определяются (20) и (21), соответственно;
определяются (20) и (21), соответственно;
2)  (23)
(23)
Теорема 13. Уравнение (23) имеет единственное решение для любого
 .
.
Доказательство утверждений теорем 12, 13 проводится аналогично доказательству теорем 10, 11 §2, поэтому их не приводим.
3.4. Выведем теперь уравнение, описывающее эволюцию распределения вероятности длины очереди, т.е.  .
.
Теорема 14. Пусть точечные процессы  и
и  не имеют общих скачков и имеют F – интенсивности
не имеют общих скачков и имеют F – интенсивности  , соответственно.
, соответственно.
Пусть  – процесс обслуживания с обратной связью, описываемый (23), причем
– процесс обслуживания с обратной связью, описываемый (23), причем  – последовательность бернуллиевских случайных величин с
– последовательность бернуллиевских случайных величин с  , не зависящая от
, не зависящая от  , i=1,2. Пусть
, i=1,2. Пусть  .
.
Тогда  удовлетворяет уравнению:
удовлетворяет уравнению:
 (24)
(24)
Доказательство теоремы опирается на утверждение.
3.4.1. Лемма 15. Пусть выполнены условия теоремы 14. Компенсаторы процессов  ,
,  ,
,  ,
,  относительно потока
относительно потока  и меры P имеют для
и меры P имеют для  вид, соответственно:
вид, соответственно:
 .
.
Доказательство. Достаточно найти компенсатор для потока обратной связи  . Пусть
. Пусть  - предсказуемый ограниченный процесс. Очевидно, что определен интеграл Римана-Стилтьеса
- предсказуемый ограниченный процесс. Очевидно, что определен интеграл Римана-Стилтьеса  и существует
и существует  . Так как
. Так как  – последовательность бернуллиевских случайных величин, то ясно, что
– последовательность бернуллиевских случайных величин, то ясно, что

Отсюда следует утверждение леммы.
3.4.2. Доказательство теоремы 14 почти дословно повторяет доказательство теоремы 10, поэтому его не приводим.
3.5. Возникает вопрос о том, можно ли предложить некоторую методику, позволяющую строить решение уравнения (17) ((24)). Такая методика существует для случая, когда коэффициенты уравнения (17) не зависят от n и t, т.е.  и основана на использовании производящих функций распределения
и основана на использовании производящих функций распределения  . Напомним, производящая функция для распределения вероятностей
. Напомним, производящая функция для распределения вероятностей  определяется выражением:
определяется выражением:
 ,
,
где  . Умножим левую и правую части (17) на
. Умножим левую и правую части (17) на  , а затем выполним суммирование по n от нуля до бесконечности. В результате получаем уравнение в частных производных первого порядка с переменными коэффициентами
, а затем выполним суммирование по n от нуля до бесконечности. В результате получаем уравнение в частных производных первого порядка с переменными коэффициентами
 (25)
(25)
Произведем теперь преобразование Лапласа [ ] уравнения (25). Так как,
 , то в результате получим из (25)
, то в результате получим из (25)
 ,
,
где  , и
, и  .
.
Затем, беря обратное преобразование Лапласа относительно  , легко, с учетом сделанных предположений, получить, что
, легко, с учетом сделанных предположений, получить, что  для любых t, n, i имеет вид:
для любых t, n, i имеет вид:

 ,
,
где  - обобщенная функция Бесселя первого рода [15]
- обобщенная функция Бесселя первого рода [15]  , Г(l)- гамма функция [15].
, Г(l)- гамма функция [15].
В общем случае неясно как строить решение уравнения (17). Поэтому возникает проблема разработки асимптотических методов анализа систем массового обслуживания.