§2. Операторы, порождаемые вероятностями перехода МПШ.
2.1. Пусть 
– множество всех конечных мер на 
и 
.
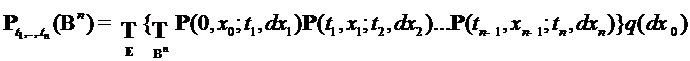- семейство переходных вероятностей некоторого марковского процесса в широком смысле. Обозначим 
, (5)
где
(6)
для любых 
и
. Ясно, что 
- двухпараметрическое семейство операторов. Из соотношения Чепмена-Колмогорова следует закон композиции операторов 
. Действительно, пусть 
, тогда в силу соотношения Чепмена-Колмогорова и теоремы Фубини, имеем:
Следовательно
. (7)
2.2. Определим, теперь, второе семейство операторов. Пусть 
- множество измеримых ограниченных функций на 
со значениями в
.
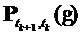, т.е. 
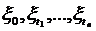. Из определения вероятности перехода следует, что 
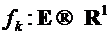- измеримая по 
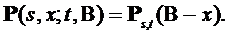функция. Если в 
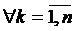ввести норму 
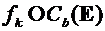, то, очевидно, 
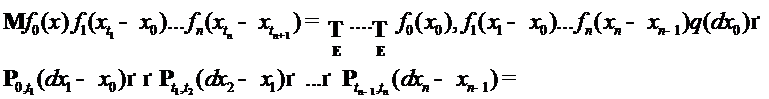. Следовательно,
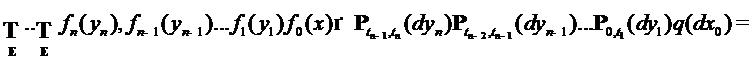– двухпараметрическое семейство операторов. Из соотношения Чепмена-Колмогорова при 
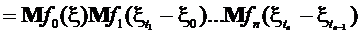следуют равенства 
Стало быть, закон композиции операторов 
имеет вид
(8)
Очевидны следующие свойства оператора
:
1)
, 2)
.
2.3. Определение. МПШ называется однородным (ОМПШ), если 
зависят только от разности 
, т.е.
(9)
Поэтому удобно ввести обозначение 
.
Для ОМПШ соотношение Чепмена-Колмогорова будет иметь вид:
В этом случае семейства операторов 
не зависят от 
и поэтому вместо двухпараметрического семейства операторов
естественно рассматривать однопараметрические семейства 
, определенные по правилам,
:
Очевидно, что:
. (10)