§ 1. Аксиоматика Колмогорова.
Определение. Пусть  .
.  - система подмножеств множества
- система подмножеств множества 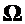 называется алгеброй если:
называется алгеброй если:
а) 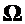 ,
, 

 ;
;
б)  А
А А
А А
А ;
;
в)  А
А
 А
А
Определение.
Пусть А - алгебра подмножества множества
- алгебра подмножества множества 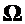 . Функция
. Функция 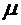 : А
: А
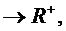 где
где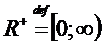 , называется конечно аддитивной мерой на А
, называется конечно аддитивной мерой на А , если
, если 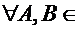 А
А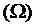
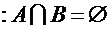 выполняется
выполняется 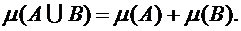
Конечно аддитивная мера называется конечной, если  .
.
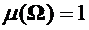 .
. Определение. Тройка  А
А ,Р), где
,Р), где 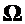 - некоторое множество, А
- некоторое множество, А - алгебра подмножества множества
- алгебра подмножества множества 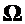 , Р - конечно аддитивная вероятностная мера на А
, Р - конечно аддитивная вероятностная мера на А , называется вероятностной моделью в широком смысле.
, называется вероятностной моделью в широком смысле.
Для построения конструктивной математической теории, такое определение вероятностной модели является слишком широким.
Определение. Система F- подмножеств множества 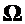 называется
называется  алгеброй, если:
алгеброй, если:
1) она является алгеброй,
2)  , для
, для  то
то  и
и  .
.
Определение . 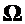 с
с  алгеброй F называется измеримым пространством и обозначается (
алгеброй F называется измеримым пространством и обозначается (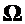 ,F).
,F).
Определение . Конечно аддитивная мера 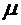 задана на А
задана на А называется счетно аддитивной (
называется счетно аддитивной ( аддитивной) мерой (или просто мерой), если из того, что для любых попарно непересекающихся множеств А1, А2, … из А
аддитивной) мерой (или просто мерой), если из того, что для любых попарно непересекающихся множеств А1, А2, … из А таких, что
таких, что  А, следует, что
А, следует, что 
Счетно аддитивная мера 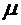 на F называется
на F называется  конечной, если
конечной, если  можно представить в виде
можно представить в виде  где
где  А
А с
с 
Счетно аддитивная мера Р на алгебре А , удовлетворяющая условию Р
, удовлетворяющая условию Р называется вероятностной мерой определенной на множествах алгебры А
называется вероятностной мерой определенной на множествах алгебры А .
.
Приведем некоторые свойства вероятностных мер:
1) 
2) если  А
А Р
Р Р
Р Р
Р Р
Р .
.
3) если  А
А и
и  Р
Р Р
Р .
.
4) Если  А
А n=1,2,.. и
n=1,2,.. и  А
А Р
Р . Задача1: Докажите первые три свойства самостоятельно. Доказательство свойства 4. Заметим, что
. Задача1: Докажите первые три свойства самостоятельно. Доказательство свойства 4. Заметим, что  , где
, где  при
при  и
и  ,
,  .Очевидно, что
.Очевидно, что  при
при  и так как
и так как  , то имеем
, то имеем  .
.
Вопрос: Когда конечно аддитивная мера является счетно аддитивной?
Теорема 1. Пусть P - конечно аддитивная функция множеств, заданная на А с
с  =1.
=1.
1) P - аддитивна;
аддитивна;
2) Р – непрерывна сверху (то есть, если 
 =1,2,…,где
=1,2,…,где  А
А ,
,
такие что  и
и  А
А , то
, то  ;
;
3) Р – непрерывна снизу (то есть, если  А
А ,
,  =1,2,…
=1,2,…  и
и  А
А , то
, то  ;
;
4) Р – непрерывна в нуле (если  А
А ,
,  =1,2,…,
=1,2,…,  и
и  O, то
O, то  .
.
Определение. Тройка (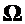 , F, Р ) называется вероятностной моделью или вероятностным пространством, где
, F, Р ) называется вероятностной моделью или вероятностным пространством, где 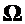 называется пространством исходов или пространством элементарных событий, множества
называется пространством исходов или пространством элементарных событий, множества  – событиями, где F -
– событиями, где F -  алгебра на
алгебра на  , а Р(А) – вероятностью события А.
, а Р(А) – вероятностью события А.