Вычисление радиуса сходимости.
Теорема. Если существует предел  , то радиус сходимости ряда равен
, то радиус сходимости ряда равен  , то есть
, то есть  , причем считаем
, причем считаем  , если
, если  , и
, и  , если
, если  .
.
Доказательство.
Предположим, что  , то есть рассмотрим числовой ряд
, то есть рассмотрим числовой ряд  , который является рядом абсолютных величин данного степенного ряда.
, который является рядом абсолютных величин данного степенного ряда.
Тогда  :
:
1. Пусть  - конечное число, отличное от нуля, значит,
- конечное число, отличное от нуля, значит,  . По радикальному признаку Коши ряд, составленный из абсолютных величин ряда, сходится при
. По радикальному признаку Коши ряд, составленный из абсолютных величин ряда, сходится при  , отсюда следует, что
, отсюда следует, что 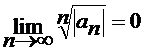 . При
. При  и
и 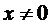 ряд расходится для всех значений
ряд расходится для всех значений  .
.
В самом деле, если бы при  ,
,  , ряд сходился, то по теореме Абеля для
, ряд сходился, то по теореме Абеля для  , где
, где  , он должен был бы сходиться, чего быть не может.
, он должен был бы сходиться, чего быть не может.
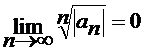 и расходится при
и расходится при 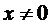 и, значит,
и, значит, 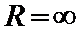 .
. 2. Пусть  . Тогда
. Тогда  при всяком значении
при всяком значении  , и ряд сходится для любого
, и ряд сходится для любого  . Значит, ряд абсолютно сходится во всякой точке оси
. Значит, ряд абсолютно сходится во всякой точке оси  и
и  .
.
3. Пусть  . Тогда
. Тогда  при всяком значении
при всяком значении  ,
,  , и значит, ряд не может сходиться ни при каком
, и значит, ряд не может сходиться ни при каком  . На основании теоремы Абеля заключаем, что ряд во всех точках оси
. На основании теоремы Абеля заключаем, что ряд во всех точках оси  (кроме нулевой) расходится и
(кроме нулевой) расходится и  .
.
Теорема. Если  , то радиус сходимости ряда равен
, то радиус сходимости ряда равен  , то есть
, то есть  , причем мы считаем
, причем мы считаем  при
при  и
и  при
при  .
.
Степенные ряды в области сходимости сходятся абсолютно и поэтому можно использовать признаки сходимости рядов с положительными членами.
По признаку Даламбера:


Ряд сходится, если  , отсюда радиус сходимости -
, отсюда радиус сходимости -  .
.
По интегральному признаку Коши:


Ряд сходится, если  , отсюда следует, что
, отсюда следует, что  .
.
Пример. Найдите область сходимости рядов: 1)  и 2)
и 2)  .
.
1)  .
.
Интервал сходимости 
Исследуем граничные точки.
 расходится;
расходится;
 - сходится условно по признаку
- сходится условно по признаку
Лейбница.
Область сходимости ряда  .
.
2)  , ряд сходится при всех
, ряд сходится при всех  .
.