Свойства равномерно сходящегося ряда.
1. Сумма равномерно сходящегося ряда в некоторой области 
, составленного из непрерывных функций, является функцией непрерывной в этой области.
2. Такой ряд можно почленно дифференцировать
.
3. Ряд можно почленно интегрировать
.
Для того чтобы определить является ли функциональный ряд равномерно сходящимся, надо воспользоваться достаточным признаком сходимости Вейерштрасса.
Определение. Функциональный ряд 
называется мажорируемым в некоторой области изменения 
, если существует такой сходящийся числовой ряд 
с положительными членами, что для всех 
из этой области выполняются неравенства 
.
Признак Вейерштрасса (равномерной сходимости функционального ряда).
Функциональный ряд сходится равномерно в области сходимости, если он является мажорируемым в этой области.
Другими словами, если функции 
в некоторой области 
не превосходят по абсолютной величине соответствующих положительных чисел 
и если числовой ряд 
сходится, то функциональный ряд 
в этой области сходится равномерно.
Пример.
Доказать равномерную сходимость функционального ряда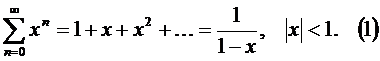
. Решение. 
. Заменим общий член этого ряда общим членом числового ряда, но превосходящего каждый член ряда по абсолютной величине. Для этого надо определить 
, при котором общий член ряда будет максимальным.
.
.
Тогда 
.
Полученный числовой ряд сходится, значит, функциональный ряд сходится равномерно согласно признаку Вейерштрасса.
Пример. Найдите сумму ряда 
.
Для нахождения суммы ряда воспользуемся известной формулой для суммы геометрической прогрессии
Дифференцируя левую и правую части формулы (1), получим последовательно
Выделим в сумме, подлежащей вычислению, слагаемые, пропорциональные первой и второй производной:
.
Вычислим производные:
тогда 