Пример 3. Целевое программирование
Провести оптимизацию вектор – функции 
 |
при ограничениях
 |
Рис.
5.3. Данные для решения примера 3.Решение. Введем данные на рабочий лист в соответствии с Рис. 5.3.
Отведем под значения переменных ячейки A20 и B20; введем формулы, определяющие ограничения задачи, в ячейки A16:A17; формулы для расчета функций 
в ячейки E20, G20 и I20, а формулу для расчета 
- в ячейку C28. Поскольку наши функции нелинейны, в окне диалога Параметры поиска решения необходимо снять флажок (указатель) линейная модель.
Далее последовательно проводим поиск оптимальных (максимальных) значений функций (целевыми ячейками выбираем E20, G20 и I20); после нахождения оптимальных значений каждой из функций ее максимальное значение заносим (используя специальную вставку) в ячейки E24, G24 и I24 соответственно. Таким образом, в ячейках окажутся значения: 1.0748 (E24), 0.7357 (G24), 2 (I24).
После этого переходим к заключительному этапу. Оптимизируем (минимизируем) значение целевой функции 
(целевая ячейка С28). Поиск решения дает для оптимального значения целевой функции значение 0,32534.
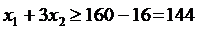, соответствующие значениям 
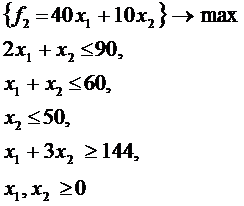, при которых отклонение 
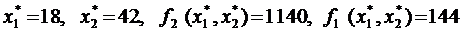от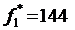 
будет минимальным. Таким образом, при данных значениях весовых коэффициентов мы получаем следующие оптимальные (с точки зрения достижения оптимального значения “совокупной” функции 
) значения компонент вектор функции:
 |  |  |  |  |  |
| 1,0748 | 0,7815 | 0,7358 | 0,3609 | 2 | 1,6784 |
Из вышеприведенной таблицы видно, что в результате оптимизации значения всех трех функций-составляющих уменьшились. Естественно, при использовании других весовых коэффициентов мы получили бы другие значения 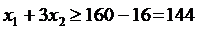(но при любых значениях весовых коэффициентов тенденция уменьшения всех компонент вектор-функции сохраняется).
Следует отметить, что задача целевого программирования может формулироваться несколько иным образом.
ЛПР может просто указать, исходя из своих соображений, желательные с его точки зрения, значения
, или диапазоны, в которых эти значения должны быть локализованы. При этой постановке задача решается практически аналогично, с тем отличием, что поиск оптимальных значений компонент (первая часть решения) не проводится, а их значения (или диапазоны изменения) вводятся в качестве ограничений дополнительно к исходным ограничениям задачи. Контрольные вопросы к теме:
1. Понятие векторного критерия
2. Типы многокритериальных задач
3. Проблемы нормализации, выбора принципа оптимальности, учета приоритета критериев, вычисления оптимума
4. Перечислите способы преобразований критериев к безразмерному виду
5. Принцип оптимальности Парето
6. Принцип равновесия по Нэшу
7. Перечислите главные особенности равновесных (по Нэшу) ситуаций
8. Конфликты, переговоры и компромиссы
9. Методы решения задач векторной оптимизации