2.1. Определение предела функции
Число а называется пределом функции  при
при  , если для
, если для  такое, что для
такое, что для  , для которых
, для которых  , выполняется неравенство
, выполняется неравенство  .
.
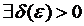 .
. Число а называется левосторонним пределом функции f(x) при  (слева), если для
(слева), если для 
 такое, что для
такое, что для  , для которых
, для которых  , выполняется неравенство
, выполняется неравенство  .
.
Число а называется правосторонним пределом функции f(x) при  (справа), если для
(справа), если для 
 такое, что для
такое, что для  , для которых
, для которых  , выполняется неравенство
, выполняется неравенство  .
.
Односторонние пределы удобно обозначать так:


Необходимое и достаточное условие существования предела с помощью односторонних пределов можно записать так:

Предел на бесконечности (при  ).
).
Число a называется пределом функции f (x) при  (или
(или  , если для
, если для  такое, что для
такое, что для  , для которых
, для которых  , выполняется неравенство
, выполняется неравенство  .
.
Пример 2.1. Доказать (найти  , что:
, что:
а)  , б)
, б) 
Решение. а) Надо доказать, что для  , для которых
, для которых  , выполняется неравенство
, выполняется неравенство  для
для  . Имеем:
. Имеем:

Примем  .
.
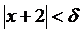 .
. Итак, для 
 такое, что
такое, что  для
для  , для которых
, для которых  .
.
б) Пусть  ,
, 
Тогда 
Здесь в числителе пользуемся неравенством  а в знаменателе пользуемся неравенством
а в знаменателе пользуемся неравенством  .
.
Пусть  . Тогда
. Тогда  .
.
Итак, для 
 такое, что неравенство
такое, что неравенство  выполняется для всех x, для которых
выполняется для всех x, для которых  .
.