2.5. Вычисление напряжённости поля заряженного шара
Пусть шар радиусом R0 заряжен с объёмной плотностью r = Q/V, которая постоянна по всему его объёму V. Найдём напряжённость внутри шара, на его поверхности и вне его (рис.
2.9). Рассматриваемый пример весьма наглядно позволяет понять, что построение вспомогательной поверхности определяется поставленной задачей. Заряд, находящийся внутри этой поверхности, тоже от неё зависит. Итак, найдём вначале напряжённость на расстоянии r1 < R0 от центра шара. Решение начинаем с построения силовых линий, направленных по силе, дейст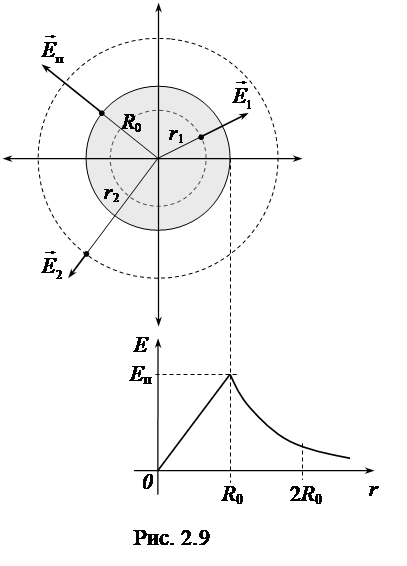
вующей на пробный заряд, вносимый в различные точки поля. Очевидно, они будут расходящимися линиями, имеющими начало в центре шара. Значит, вспомогательная поверхность должна иметь форму сферы произвольного радиуса r1. Она перпендикулярна силовым линиям и проходит через точку, в которой определяется напряжённость. Внутри этой сферы будет находиться не весь заряд шара, а лишь часть его, равная 
, то есть заряд внутри равен объёмной плотности заряда, умноженной на объём шара радиусом r1. Согласно теореме Гаусса поток через эту сферу
 . | (2.31) |
Связь напряжённости с потоком через проведённую поверхность сферы может быть записана с учётом её перпендикулярности силовым линиям:
 . | (2.32) |
Приравняв потоки, получим формулу для вычисления напряженности:
 . | (2.33) |
Напряжённость поля оказалась прямо пропорциональной расстоянию от центра шара, отмеряемому по силовой линии.
На графике (см. рис 2.9) по оси абсцисс отложено расстояние r от центра шара, и проведена прямая, характеризующая зависимость E(r) для рассматриваемого случая r < R0 .Теперь найдём напряжённость на поверхности шара. Проведённая для этого вспомогательная поверхность совпадает с поверхностью шара, а внутри неё будет находиться заряд 
. Теорема Гаусса будет выглядеть так:
 . | (2.34) |
Поток через выбранную поверхность также изменится:
 , | (2.35) |
где Eп — напряжённость теперь уже на поверхности шара. Приравняв потоки, получим
 . | (2.36) |
Значение Eп отложено на графике, задавая ту точку, которая ограничивает рост напряжённости внутри шара по мере увеличения расстояния от его центра.
Наконец найдём напряжённость поля вне заряженного шара, то есть для точек, находящихся от центра шара на расстоянии r2 > R0. Проводя вспомогательную поверхность через точку на расстоянии r2 от центра (см. рис. 2.9), убеждаемся, что она, как и в первых двух случаях, имеет форму сферы и перпендикулярна всюду силовым линиям. Внутри неё будет заключён весь заряд шара, и теорема Гаусса будет выражена, как и во втором случае, уравнением (2.34) с той лишь разницей, что в качестве радиуса сферы выступает r2.
 . | (2.37) |
Совмещая (2.34) с полученным выше равенством будем иметь
 . | (2.38) |
Напряжённость вне заряженного шара убывает пропорционально квадрату расстояния r от центра, и на r = 2R0 будет в четыре раза меньше максимальной.