4.7. Волны
Волна – очень распространённый вид движения. Мы хорошо знакомы с волной, распространяющейся по поверхности воды. Колебания частиц воздуха, вызываемые колебаниями голосовых связок или диафрагм громкоговорителей, передаются от одной частицы к другой и в воздухе распространяется звуковая волна.
Если она распространяется во все стороны в однородной среде, её называют сферической. В этом случае колебания, переносимые волной, распространяются во все стороны одинаково, и совокупность точек, до которых одновременно дошло колебательное движение, образует сферу, в центре которой находится источник колебания.Простейший вид волнового движения – это волны, распространяющиеся в одном направлении. Такие волны можно, например, вызвать, если ударить по одному из концов упругого стержня. Колебания дойдут одновременно до точек, лежащих на плоскости, перпендикулярной той оси, вдоль которой идет колебание. Волна в этом случае носит название плоской. Совокупность же точек, до которых одновременно дошли колебания, носит название фронта волны. В первом случае фронт волны – сфера, во втором – плоскость.
Различают ещё волны поперечные и продольные. У поперечных волн колебания точек происходят перпендикулярно направлению распространения волны, у продольных волн – вдоль него. Поскольку волна есть распространяющееся колебательное движение, уравнение её можно получить на основе уравнения (4.1), описывающего колебательное движение.
Пусть уравнение движения источника колебаний имеет вид:
 . . | (4.47) |
Здесь время измеряется от начала колебаний этого источника. Пусть волна будет плоской и распространяться вдоль оси l. Как и любой процесс, передача колебательного движения от одной точки к другой требует времени. Иначе говоря, волна распространяется в среде с определенной скоростью –  .
.
В случае, если мы хотим рассчитывать смещение от положения равновесия не только самого источника колебаний, но и любой точки на оси l, следует в упомянутом уравнении время t заменить временем t' колебания той точки, смещение которой мы хотим рассчитать. Очевидно, что оно будет равно:
 , , | (4.48) |
то есть будет зависеть от того, на каком расстоянии по оси от источника выбрана точка. Последнее является вполне естественным, поскольку чем дальше от источника расположена эта точка, тем больше времени нужно, чтобы колебания дошли до неё.
Уравнение плоской волны, т.е. уравнение колебаний любой точки оси l получается из уравнения (4.49) при замене времени t на время t':
 | (4.49) |
Часто это уравнение записывают несколько иначе, используя понятие длины волны. Последней называют то расстояние, которое волна проходит за время, равное периоду:
 . . | (4.50) |
Заменив угловую частоту в уравнении волны через период и внеся её в круглые скобки, получим:
 . . | (4.51) |
|
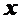 есть периодическая функция и той, и другой величины. Поэтому уравнение волны помимо развёртки колебаний во времени, записанной для точки с координатой l, будет иметь ещё один график – зависимость
есть периодическая функция и той, и другой величины. Поэтому уравнение волны помимо развёртки колебаний во времени, записанной для точки с координатой l, будет иметь ещё один график – зависимость 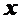 от координаты l.
от координаты l.   |
Оба эти графика изображены на рис. 4.9. Верхний получен при фиксированной координате, нижний – при фиксированном времени. В зависимости от того, какая величина отложена по горизонтальной оси, из графика можно найти либо период колебаний T, либо длину волны  .
.
Так же, как и в случае колебательного движения, приведенное выше уравнение (4.51) в строгой теории колебаний называют решением волнового дифференциального уравнения. В разделе 4.2 было получено дифференциальное уравнение второго порядка для колебательного движения (4.9) – уравнение второго закона Ньютона, записанное для этого случая.
Оно содержит ускорение – вторую производную от смещения 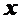 по времени. В случае волнового движения должна добавиться ещё одна производная – по координате l. Поскольку нам уже известно решение уравнения волны, пойдём путём, обратным тому, которым идут в строгой теории: по решению (4.51) найдем вид волнового дифференциального уравнения. Для этого дважды продифференцируем (4.51) по t , а затем по l , сначала считая постоянным l , а потом – t:
по времени. В случае волнового движения должна добавиться ещё одна производная – по координате l. Поскольку нам уже известно решение уравнения волны, пойдём путём, обратным тому, которым идут в строгой теории: по решению (4.51) найдем вид волнового дифференциального уравнения. Для этого дважды продифференцируем (4.51) по t , а затем по l , сначала считая постоянным l , а потом – t:
 ; ;  . . | (4.52) |
Следовательно, умножая на величину  вторую частную производную от смещения по времени, мы получим вторую производную по координате от этой же величины:
вторую частную производную от смещения по времени, мы получим вторую производную по координате от этой же величины:
 . . | (4.53) |
Как и следовало ожидать, дифференциальное уравнение волны содержит две частных производных, а не одну, как в случае колебательного движения.