6.5. Смысл постоянной a
Постоянная 
в распределении молекул по проекциям скоростей введена по соображениям размерности при подборе вида функции распределения.
Хорошо известно, что давление определяется двумя макрохарактеристиками – температурой и концентрацией (6.20). Вместе с тем, зная функцию распределения по проекциям скоростей, его можно связать с характеристиками движения каждой молекулы – проекцией ее скорости, массой. Действительно, газ оказывает давление на стенки сосуда, поскольку молекулы, ударяясь о стенку и отскакивая от нее, каждая действует на стенку с силой f0. Эта сила будет тем больше, чем быстрее двигалась молекула по направлению к стенке. Поэтому давление p разумнее всего вычислять как
 , | (6.43) |
где dp - давление, создаваемое ударами молекул, скорости которых близки друг другу, т.е. лежат в достаточно малом интервале скоростей dux. Индекс означает, разумеется, что рассматривать следует проекции скоростей, чтобы можно было считать молекулы летящими только вдоль осей, перпендикулярных стенкам.
Если всего вдоль оси x движется N молекул, то только dN молекул будут иметь выделенную нами скорость. Поскольку давление – это сила, действующая на единицу площади, то, обозначив через f0 силу удара одной молекулы и через dS – элемент площади, получим:
 . | (6.44) |
Задача теперь сводится к нахождению двух величин: dN и f0. Сила удара молекулы может быть найдена по второму закону Ньютона:
 , | (6.45) |
 . | (6.46) |
где m0 – масса одной молекулы.
Вектор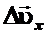
(рис. 6.6.) найден по правилу вычитания векторов, и его длина равна двум uх, поскольку удар изменил лишь направление скорости, оставив величину ее неизменной. Тогда:  |
 |
Теперь найдем dN из следующих соображений: так как скорости разложены на составляющие, можно представить, что все молекулы движутся лишь вдоль осей. Выделим на стенке сосуда элемент площади dS (рис. 6.7). О поверхность dS будут ударяться лишь те молекулы, которые находятся в объеме длиной uxDt и площадью dS. Те молекулы, которые находятся за пределами этого объема, не ударятся о стенку, если даже они будут двигаться по направлению к ней (молекулы, находящиеся на расстоянии l > uxDt, за Dt секунд не успеют подлететь к dS). Следовательно,
| dN = uxDt?dS?dn. | (6.47) |
Если n – концентрация всех молекул, то dn – это концентрация молекул, обладающих выбранным нами значением ux. Согласно определению, вероятность найти такие молекулы будет:
 , | (6.48) |
где f (
) – функция распределения молекул по проекциям скоростей. Подставляя в (6.44) силу по (6.46), dN по (6.47) и, наконец, dn по (6.48), получим:
 , | (6.49) |
или, используя полученное выше значение функции распределения по (6.41):
 . | (6.50) |
Интегрируя в пределах от 0 до р во всем интервале скоростей, получим:
  | (6.51) |
Если воспользоваться для нахождения значения интеграла уравнением (6.39.2), будем иметь:
 . | (6.52) |
Воспользовавшись известным выражением для давления через концентрацию и температуру (6.21), получим окончательно:
 . | (6.53) |