1.2. Примеры решения задач
Пример 1. Движение материальной точки задано уравнением
|
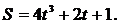
Найдите мгновенные значения скорости и ускорения в конце первой и второй секунд движения, среднюю скорость за вторую секунду.
Решение. Мгновенную скорость находим как производную от координаты по времени:
|
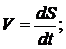
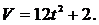
Для вычисления средней скорости движения надо найти отношение пути ко времени, в течение которого он пройден:
|
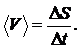
По формуле (2) вычисляем скорости в указанные моменты времени (t1 = 1 c, t2 = 2 c):


Для определения средней скорости находим путь, проходимый за время от t0 = 1 c до t = 2 c, используя уравнение (1):


По формуле (3) вычисляем:


Мгновенное ускорение определяется первой производной от скорости по времени или второй производной от координаты по времени:



Используя формулу (2), находим а.
В указанные моменты времени ускорение равно а1 = 24 м/с2 и а2 = 48 м/с2.Ответ: в момент времени t1 = 1 c и t2 = 2 c мгновенные скорости и ускорения соответственно равны V1 = 14 м/с, V2 = 50 м/с, а1 = 24 м/с2, а2 = 48 м/с2, средняя скорость за вторую секунду 
Пример 2. Тело брошено вверх с высоты 12 м под углом 30° к горизонту с начальной скоростью 12 м/с. Определить продолжительность полета тела до точки А и до точки В (рис. 1), максимальную высоту, на которую поднимается тело, дальность полета тела. Сопротивление воздуха не учитывать.
Дано: Н = 12 м, j = 30°, V0 = 12 м/с.
Найти: tA; tB; Hmax; Smax.
Решение. Из уравнения скорости равнопеременного движения  определяем проекции вектора скорости на координатные оси (рис. 1.1), учитывая, что
определяем проекции вектора скорости на координатные оси (рис. 1.1), учитывая, что 
|
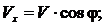
|
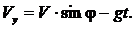

Рис. 1.1
Положение тела с течением времени изменяется в соответствии с уравнением равнопеременного движения:  в проекциях на координатные оси:
в проекциях на координатные оси:
|
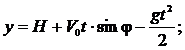
|
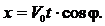
Изменения координаты тела Dy связаны с проекциями скорости и ускорения выражением
|
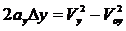 или
или 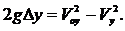
Время полета тела до точек А и В найдем из уравнений (3), подставив соответствующие координаты (yA = h, yB = 0):
|
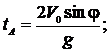
|
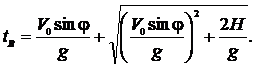
Дальность полета найдем из уравнения (4), подставив в него время движения из уравнения (7):
|
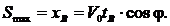
Для определения максимальной высоты подъема учтем, что в наивысшей точке с y = Hmax Vy = 0, тогда из формулы (5) при Dy = Hmax – H получим:
|
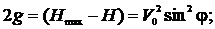

Тогда [см.
(6)–(9)]:



Ответ: время движения до точки А tA = 1,2 с, до точки В tВ = 2,3 с, наибольшая высота подъема Нmax = 13,84 м, дальность точки падения Smax = 23,8 м.
Пример 3. По условию примера 2 найти в момент приземления тела следующие величины: скорость и угол падения тела; тангенциальное и нормальное ускорение тела; радиус кривизны траектории.
Дано: Н = 12 м, j = 30°, V0 = 12 м/с.
Найти: VВ; b; аt; аn; R.
Решение. Мгновенная скорость в точке В (см. рис. 1.1, 1.2) находится по значениям проекций скорости в данной точке:
|
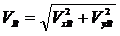 или
или 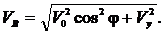
Значение VхВ определяется по уравнению (1) примера 2:

Vy в точке В найдем из уравнения (5) примера 2, подставив в него:



Из уравнения (1) получим
|
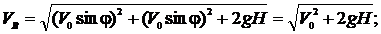


Рис. 1.2
Для определения угла b, составленного вектором скорости VВ с горизонтальной осью ОХ, воспользуемся рис.
1.2.


Тангенциальная составляющая ускорения  направлена вдоль вектора мгновенной скорости в данной точке, т.е. по касательной к траектории. Нормальная составляющая ускорения
направлена вдоль вектора мгновенной скорости в данной точке, т.е. по касательной к траектории. Нормальная составляющая ускорения  направлена перпендикулярно вектору мгновенной скорости VB. Полное ускорение равно их векторной сумме
направлена перпендикулярно вектору мгновенной скорости VB. Полное ускорение равно их векторной сумме 
Тогда





Радиус кривизны траектории в точке приземления определяем из уравнения нормального ускорения:



Ответ: скорость в точке падения VB = 19,5 м/с, угол падения  тангенциальное ускорение at = 8,3 м/с2, нормальное ускорение an = 5,25 м/с2, радиус кривизны траектории R = 72,5 м.
тангенциальное ускорение at = 8,3 м/с2, нормальное ускорение an = 5,25 м/с2, радиус кривизны траектории R = 72,5 м.
Пример 4. На двух шнурах одинаковой длины, равной 0,8 м, подвешены два свинцовых шара массами 0,5 и 1 кг. Шары соприкасаются между собой. Шар меньшей массы отвели в сторону так, что шнур отклонился на угол a = 60°, и отпустили.
На какую высоту поднимутся оба шара после столкновения? Удар считать центральным и неупругим. Определить энергию, израсходованную на деформацию при ударе.Дано: m1 = 0,5 кг, m2 = 1 кг, a = 60°, l = 0,8 м.
Найти: h, DW.
Решение. Так как удар шаров неупругий, то после удара шары будут двигаться с общей скорость  Закон сохранения импульса для этого удара имеет вид:
Закон сохранения импульса для этого удара имеет вид:

где  – скорости шаров до удара.
– скорости шаров до удара.
Или с учетом направлений и величин скоростей:
|
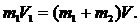
Скорость меньшего шара V1 найдем, используя закон сохранения энергии. При отклонении меньшего шара на угол a (рис. 1.3) мы сообщаем ему запас потенциальной энергии, которая затем переходит в кинетическую:


Рис. 1.3
Из рис. 1.3 видно, что  поэтому
поэтому
|
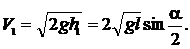
Из уравнений (1) и (2) находим скорость шаров после удара:
|
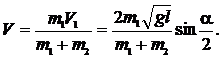
Кинетическая энергия, которой обладают шары после удара, переходит в потенциальную:

Отсюда определяем высоту поднятия шаров после столкновения:

|
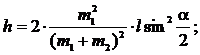

При неупругом ударе шаров часть энергии расходуется на деформацию.
Энергия деформации определяется разностью энергий системы до и после удара:
Используя уравнения (2) и (3), получаем:


Ответ: высота поднятия шара h = 0,044 м, энергия деформации DWд = 1,3 Дж.
Пример 5. Тонкий стержень массой 300 г и длиной 50 см вращается с угловой скоростью 10 с–1 в горизонтальной плоскости вокруг вертикальной оси, проходящей через середину стержня. Продолжая вращаться в той же плоскости, стержень перемещается так, что ось вращения теперь проходит через конец стержня. Найти угловую скорость во втором случае.
Дано: m = 300 г = 0,3 кг, l = 50 см = 0,5 м, w = 10 с–1.
Найти: w2.
Решение. Используем закон сохранения момента количества движения:
|
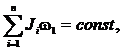
где Ji – момент инерции стержня относительно оси вращения.
Для изолированной системы тел векторная сумма моментов импульса относительно оси вращения остается постоянной. В данной задаче, вследствие того, что распределение массы стержня относительно оси вращения изменяется, момент инерции стержня также изменяется, но при этом в соответствии с уравнением (1) момент импульса постоянен:
|
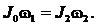
Момент инерции стержня относительно оси, проходящей через центр масс и перпендикулярной стержню (1-й случай), равен:
|
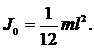
По теореме Штейнера
|
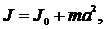
где J – момент инерции тела относительно произвольной оси вращения; J0 – момент инерции относительно параллельной оси, проходящей через центр масс; a – расстояние от центра масс до выбранной оси вращения.
Найдем момент инерции относительно оси, проходящей через конец стержня и перпендикулярной ему (2-й случай). Так как  из (3) и (4) получим
из (3) и (4) получим
|
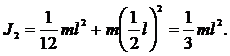
Подставим формулы (3) и (5) в (2):



Ответ: угловая скорость во втором случае w2 = 2,5 с–1.
Пример 6. Материальная точка массой 20 г совершает гармонические колебания с периодом 9 с. Начальная фаза колебания 10°. Через сколько времени от начала движения смещение точки достигнет половины амплитуды? Найти амплитуду, максимальные скорость и ускорение точки, если ее полная энергия равна 10–2 Дж.
Дано: m = 20 г = 2?10–2 кг; T = 9 с; 
 W = 10–2 Дж.
W = 10–2 Дж.
Найти: t, A, Vmax, amax.
Решение. Уравнение гармонического колебательного движения:
|
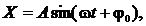 или
или 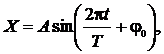
где Х – смещение точки относительно положения равновесия; А – амплитуда колебания;  – циклическая частота; T – период колебаний; t – время колебания; j0 – начальная фаза колебания.
– циклическая частота; T – период колебаний; t – время колебания; j0 – начальная фаза колебания.
Из уравнения (1) можно определить время колебания:


Из формулы полной энергии колеблющейся точки  определим амплитуду ее колебаний:
определим амплитуду ее колебаний:


Зная амплитуду, можно вычислить максимальную скорость точки, которая определяется как первая производная от смещения по времени:

Так как максимальное значение  получаем:
получаем:


Ускорение точки определяется как первая производная скорости по времени:

Максимальное значение  следовательно:
следовательно:


Ответ: время, через которое отклонение равно половине амплитуды, t = 0,5 с; амплитуда А = 1,43 м; наибольшая скорость Vmax = 1 м/с; наибольшее ускорение аmax = 0,7 м/с2.
Пример 7. Какую минимальную скорость нужно сообщить ракете, чтобы она не вернулась на Землю, преодолев земное тяготение? Сопротивление атмосферы не учитывать.
Решение. С удалением ракеты от Земли будет увеличиваться ее потенциальная энергия  и уменьшаться кинетическая
и уменьшаться кинетическая  По закону сохранения энергии: уменьшение кинетической энергии равно увеличению потенциальной.
По закону сохранения энергии: уменьшение кинетической энергии равно увеличению потенциальной.
|
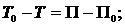

где m – масса ракеты; M – масса Земли; G – гравитационная постоянная; V0, V – скорость ракеты относительно Земли в начальный и в рассматриваемый моменты; R0, R – расстояние от центра Земли до ракеты в начальный и в рассматриваемый моменты.
После преобразования уравнения (1) имеем:

Ракета не вернется на Землю, если ее скорость V будет равна нулю в бесконечности, т.е. V = 0 при R = ∞.
В этом случае
|
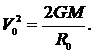
Сила тяготения равна силе тяжести на поверхности Земли:
|
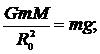
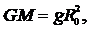
где g = 9,8 м/с2 – ускорение свободного падения на поверхности Земли.
Подставляя формулу (3) в (2), находим
 или
или 
Считая, что ракета набирает нужную скорость V0 уже вблизи поверхности Земли, и полагая радиус Земли равным 6 370 км, находим

Скорость, необходимая для преодоления поля тяготения Земли, называется второй космической или параболической скоростью.
Ответ: скорость, необходимая для преодоления тяготения Земли, V0 = 11,2 км/с.
Пример 8. В сосуде емкостью 8,3 л находится воздух при нормальном давлении и температуре 300 К. В сосуд вводят 3,6 г воды и закрывают крышкой. Определить давление в сосуде при 400 К, если вся вода при этой температуре превращается в пар?
Дано: V = 8,3 л = 8,3?10–3 м3; Т0 = 300 К; m = 3,6 г = =3,6?10–3 кг; Т1 = 400 К; Р0 = 1,013?105 Па.
Найти: P.
Решение. Давление в сосуде складывается из давления воздуха, нагретого до температуры 400 К (P1), и давления водяных паров при той же температуре (P2). Из объединенного газового закона  находим давление воздуха:
находим давление воздуха:

Из уравнения Клапейрона-Менделеева  найдем давление водяных паров:
найдем давление водяных паров:

где М = 18?10–3 кг/моль – молярная масса водяного пара; R = 8,31  – универсальная газовая постоянная.
– универсальная газовая постоянная.
По закону Дальтона для смеси газов  найдем давление газа в сосуде:
найдем давление газа в сосуде:

Тогда

Ответ: давление Р = 2,15?105 Па.
Пример 9. Определить плотность разреженного азота, если средняя длина свободного пробега молекул 10 см. Какова концентрация молекул?
Дано:  = 10 см = 0,1 м.
= 10 см = 0,1 м.
Найти: r, n0.
Решение. Средняя длина свободного пробега молекул определяется формулой
|
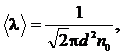
где d – эффективный диаметр молекулы (для азота d = 0,3?10–9 м).
Концентрацию молекул определим из равенства
|
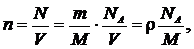
где NA = 6,02?1023 моль–1 – постоянная Авогадро; M = 28?10–3 кг/моль – молярная масса азота;  – плотность газа.
– плотность газа.
Решая совместно уравнения (1) и (2), находим:




Ответ: плотность газа r = 1,16?10–6 кг/м3; концентрация n = 2,49?1019 м–3.
Пример 10. Наружная поверхность кирпичной стены площадью 25 м2 и толщиной 37 см имеет температуру 259 К, а внутренняя поверхность – 293 К. Помещение отапливается электроплитой. Определить ее мощность, если температура в помещении поддерживается постоянной. Теплопроводимость кирпича 0,4 
Дано: S = 25 м2; d = 37 см = 0,37 м; Т1 = 259 К; Т2 = 293 К; c = 0,4 
Найти: N.
Решение. Количество теплоты, прошедшее через наружную стену, определить по закону Фурье:
|
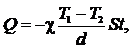
где t – время протекания теплоты.
За время t электроплита должна выделить такое же количество теплоты:
|
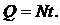
Приравнивая правые части уравнений (1) и (2), получаем:

откуда


Ответ: мощность электроплиты N = 1 кВт.
Пример 11. При температуре 250 К и давлении 1,013?105 Па двухатомный газ занимает объем 80 л. Как изменится энтропия газа, если давление увеличить вдвое, а температуру повысить до 300 К?
Дано: Р1 = 1,013?105 Па; Т1 = 250 К; V1 = 80 л = 8?10–2 м3; Р2 = 2Р1; Т2 = 300 К.
Найти: DS.
Решение. Изменение энтропии определяется формулой
|
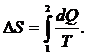
Количества теплоты находим из первого закона термодинамики:
|
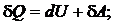

где dU – изменение внутренней энергии; dА – работа расширения газа; m – масса газа; M – молярная масса; Сv – молярная теплоемкость при постоянном объеме; dV – изменение объема газа.
Для двухатомных газов i = 5.

где R – универсальная газовая постоянная.
Величины  и Р найдем из уравнения Клапейрона–Менделеева:
и Р найдем из уравнения Клапейрона–Менделеева:
|
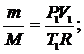

Подставляя уравнение (3) в (2), находим:
|
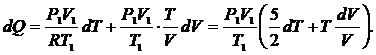
Подставляя выражение (4) в (1), находим:


тогда


Ответ: изменение энтропии DS = 1,88 Дж/К.
Пример 12. Тепловая машина работает по циклу Карно (рис. 1.4). При изотермическом расширении двухатомного газа его объем увеличивается в 3 раза, а при последующем адиабатическом расширении – в 5 раз. Определить КПД цикла. Какую работу совершает 1 кмоль газа за один цикл, если температура нагревателя 300 К? Какое количество теплоты получит от холодильника машина, если она будет совершать тот же цикл в обратном направлении, и какое количество теплоты будет передано нагревателю?
Дано: 
 v = 1 кмоль = 103 моль; Тн = Т1 = 300 К.
v = 1 кмоль = 103 моль; Тн = Т1 = 300 К.
Найти: h; А; Qн; Qх.
Решение. КПД цикла Карно определяется формулой
|
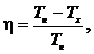
где Тн – температура нагревателя; Тх – температура холодильника.

Рис. 1.4
В адиабатном процессе 2®3 параметры состояния связаны уравнением Пуассона  или
или  следовательно,
следовательно,  так как
так как  а
а  Из равенства (1) получаем
Из равенства (1) получаем
|
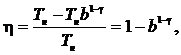
где b1–g = 51–1,4 = 0,525.
Следовательно, h = 1 – 0,525 = 0,475; h = 47,5%.
Работа цикла Карно определяется разностью теплоты Qн, полученной в процессе 1®2, и теплоты Qх, отданной в процессе 3®4:
|
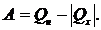
При изотермическом процессе
|
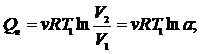

так как  (доказать самостоятельно).
(доказать самостоятельно).
Знак «минус» показывает, что теплота отдается газом холодильнику.
|
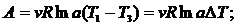

где 

Подставим числовые значения в равенство (5):

При обратном цикле Карно газ расширяется по адиабате 1®4, а затем по изотерме 4®3, получая при этом от холодильника количество теплоты Qх. Далее газ сжимается по адиабате 3®2, а затем по изотерме 2®1, отдавая при этом количество теплоты Qн. По формулам (4) находим:


Ответ: КПД h = 47,5%; работа А = 1,32 МДж. В обратном цикле количество теплоты, полученное от холодильника, Qх = 1,42 МДж, количество теплоты, переданное нагревателю Qн = –2,74 МДж.
Пример 13. Из капиллярной трубки с радиусом канала 0,2 мм по каплям вытекает жидкость. Масса 100 капель равна 0,282 г. Определить поверхностное натяжение жидкости.
Дано: r = 0,2 мм = 2?10–4 м; n = 100; m = 0,282 г = 2,82?10–4 кг.
Найти: s.
Решение. Капля отрывается в тот момент, когда ее сила тяжести равна силе поверхностного натяжения. Считая радиус шейки капли равным радиусу капилляра, для силы поверхностного натяжения можно записать

Так как масса одной капли  получим
получим

откуда


Ответ: коэффициент поверхностного натяжения s = 2,2?10–2 Н/м.