1.1. Понятие о векторах и простейших действиях над ними
Вектором называют любую физическую величину, имеющую не только числовое значение, но и направление. Двойная смысловая нагрузка вектора хорошо видна при такой записи векторной величины  :
:
 , , | (1.1) |
где число  характеризует абсолютное значение, а
характеризует абсолютное значение, а 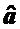 – направление.
– направление.
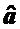 называют единичным вектором, поскольку величина его равна единице.
называют единичным вектором, поскольку величина его равна единице. Геометрически векторная величина изображается стрелкой, опять-таки несущей двойную смысловую нагрузку: длина стрелки определяет абсолютное значение векторной величины, а направление указывается стрелкой. Условимся обозначать любую векторную величину соответствующей буквой со стрелкой над ней, а модуль вектора – той же буквой без стрелки. Так, например,  – вектор скорости, а u – модуль скорости, то есть всегда величина положительная.
– вектор скорости, а u – модуль скорости, то есть всегда величина положительная.
 Действия над векторами введены из-за необходимости описывать наблюдаемые явления. Так, на рис.1.1 изображена задача, в которой из т. А в т. C можно пройти двумя путями: прямым (вектор
Действия над векторами введены из-за необходимости описывать наблюдаемые явления. Так, на рис.1.1 изображена задача, в которой из т. А в т. C можно пройти двумя путями: прямым (вектор  ) и через точку В. Во втором случае результат будет такой же, поэтому:
) и через точку В. Во втором случае результат будет такой же, поэтому:
 . . | (1.2) |
Длину вектора  , то есть абсолютное значение пути АC можно найти, если известны длины отрезков АB и ВC, то есть зная a и b (модули соответствующих векторов).
, то есть абсолютное значение пути АC можно найти, если известны длины отрезков АB и ВC, то есть зная a и b (модули соответствующих векторов).
 , , | (1.3) |
где a – угол между векторами  и
и  .
.
Углом между двумя векторами называют угол, образованный этими векторами, проведенными из одной точки. На рис. 1.1а показан не угол между векторами, а равный ему. Если пользоваться правилом параллелограмма, то на чертеже можно указать непосредственно угол между векторами соответственно его определению (см. рис. 1.1б). В теореме косинусов (1.3) знак плюс появляется потому, что сторона с лежит против угла (180о– a).
Операция сложения векторов, как видим, требует для её выполнения двух уравнений. Уравнение (1.2) формально задаёт вектор-сумму, а уравнение (1.3) даёт возможность вычислить модуль суммы двух векторов. Заметим, что само по себе выражение (1.2) не задаёт направление вектора  , а лишь определяет операцию. Это определение следует дополнить правилом сложения: сложить два вектора – значит построить второй вектор из конца первого и соединить стрелкой начало первого вектора с концом второго. Пунктиром на рис. 1.1б показано сложение по правилу параллелограмма, которое, очевидно, эквивалентно первому.
, а лишь определяет операцию. Это определение следует дополнить правилом сложения: сложить два вектора – значит построить второй вектор из конца первого и соединить стрелкой начало первого вектора с концом второго. Пунктиром на рис. 1.1б показано сложение по правилу параллелограмма, которое, очевидно, эквивалентно первому.
Этот же рисунок иллюстрирует и вычитание векторов: если результат – путь АС – известен, а пройден путь АВ, то остался путь ВС, значит:
 . . | (1.4) |
Отсюда вытекает правило вычитания векторов: соединив начала векторов и замкнув концы в сторону вектора уменьшаемого, получим вектор разности. Длина его также может быть найдена по теореме косинусов:
 . . | (1.5) |
Снова задача нахождения векторной величины  распадается на две: нахождение направления вектора по (1.4) и его модуля по (1.5).
распадается на две: нахождение направления вектора по (1.4) и его модуля по (1.5).
Здесь уместно заметить, что приращение D векторной величины – это вектор разности двух векторов. Так, скорость – векторная величина и ее изменение (приращение) будет тоже векторной величиной:
 . . | (1.6) |
Направление приращения скорости найдется по правилу вычитания векторов, и, следовательно, не будет совпадать с направлением ни вектора-уменьшаемого, ни вектора-вычитаемого. Длина вектора  записывается с символом модуля – |
записывается с символом модуля – | |. Не следует путать его с изменением длины вектора
|. Не следует путать его с изменением длины вектора  , обозначаемым через
, обозначаемым через  . Нетрудно убедиться, что если векторы направлены в одну сторону и длина вектора
. Нетрудно убедиться, что если векторы направлены в одну сторону и длина вектора  больше длины вектора
больше длины вектора  , то приращение скорости совпадет с направлением скоростей. Если же скорость
, то приращение скорости совпадет с направлением скоростей. Если же скорость  <
<  , то приращение будет отрицательно, то есть направлено в сторону, противоположную движению.
, то приращение будет отрицательно, то есть направлено в сторону, противоположную движению.
Векторы можно перемножать двумя способами: скалярным и векторным.
Скалярное произведение двух векторов есть скаляр, величина которого равна произведению модулей перемножаемых векторов, умноженному на косинус угла между ними:
 . . | (1.7) |
Скалярное умножение векторов – единственный случай действия над векторами, когда не требуется два уравнения: ведь получаемый результат – скаляр!
Результатом векторного умножения векторов будет вектор, направление которого находится по правилу: вектор векторного произведения двух векторов перпендикулярен плоскости, в которой лежат векторы-сомножители.
Направление векторного произведения определяется поступательным движением буравчика, если головку вращать от первого сомножителя ко второму (рис. 1.2). Записывается векторное произведение так:  . . | (1.8) |
Одного уравнения (1.7), указывающего операцию, вновь не достаточно: ведь следует указать и величину этого вектора. Она находится по правилу:
 , , | (1.9) |
где a – угол между векторами-сомножителями.
В механике приходится иметь дело ещё и с двойным векторным произведением, но это правило будет дано в тексте соответствующей лекции.
Кроме арифметических операций с векторными величинами часто бывает нужно находить проекции вектора на оси координат, или выражать вектор через его проекции. Рассмотрим двумерный случай, когда вектор  лежит в плоскости XOY и составляет угол a с осью ОХ (рис. 1.3). Как следует из рисунка, угол вектора
лежит в плоскости XOY и составляет угол a с осью ОХ (рис. 1.3). Как следует из рисунка, угол вектора  с осью ОУ будет в этом случае равен (90о + a). Проекциями данного вектора на оси координат будут числа ax и ay, которые определяются величиной вектора и углом a. В данном случае (см. рис. 1.3)
с осью ОУ будет в этом случае равен (90о + a). Проекциями данного вектора на оси координат будут числа ax и ay, которые определяются величиной вектора и углом a. В данном случае (см. рис. 1.3)
| ax = acosa; ay = – asina. | (1.10) |
 Вектор через его проекции можно выразить как сумму векторов, полученных умножением проекций на соответствующие единичные векторы
Вектор через его проекции можно выразить как сумму векторов, полученных умножением проекций на соответствующие единичные векторы  и
и  , выполняющие роль введенного выше единичного вектора
, выполняющие роль введенного выше единичного вектора 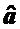 , и определяющие направления осей координат:
, и определяющие направления осей координат:
 . . | (1.11) |
Модуль вектора легко определяется через его проекции по теореме Пифагора:
 . . | (1.12) |
В трехмерном случае проекций вектора будет три и в суммах (1.11) и (1.12) добавится проекция az c соответствующим единичным вектором.
Набор сведений из векторной алгебры, используемых в физике, этим кратким знакомством не заканчивается. Мы продолжим его во второй части.