1.1. Некоторые понятия векторного анализа

Во второй части курса общей физики рассмотрим электромагнитное поле и его частные случаи — электростатическое поле и магнитное поле. При изложении ряда вопросов этого раздела мы встретимся с некоторыми новыми понятиями: потоком и циркуляцией векторной функции, а также с градиентом скалярной функции.

1. Определим элементарный поток dΦ любого вектора через бесконечно малую площадку da как скалярное произведение этого вектора на элемент поверхности или, иначе, на вектор площадки

,

(1.1)

где — внешняя нормаль к площадке da. Очевидно, что элемент поверхности направлен перпендикулярно поверхности в каждой ее точке. Руководствуясь определением потока, и обозначив его через Φ, можно записать

b?da?cosa,

(1.2)

где α — угол между вектором и нормалью, проведенной к элементу поверхности (рис. 1.1), а dF — элементарный поток вектора .

Название величины Ф — поток — взято из гидродинамики. Действительно, если 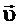— скорость текущей жидкости, а a — площадь погруженной в нее плоской сетки, то объем жидкости, протекающей через сетку в единицу времени, будет равен

то есть Ф здесь — это поток вектора скорости.

На рис. 1.2 представлены три различные ориентации этой сетки. Очевидно, что последнее равенство (1.3) может быть получено интегрированием по всей поверхности a равенства (1.2), определяющего понятие элементарного потока, при условии, что величина вектора скорости и угол a постоянны по всей поверхности.

Естественно, что понятие потока применимо к любому множеству векторов, имеющих тот или иной физический смысл. Мы воспользуемся этим понятием дважды — изучая электростатическое и магнитное поля.

2. Понятие, к рассмотрению которого мы теперь переходим, несколько более сложно. Пусть имеется совокупность векторов , различной длины и направления, и задана некоторая кривая L, которую можно разбить на элементы (рис. 1.3). Требуется найти сумму скалярных произведений вектора на соответствующий ему элемент перемещения 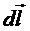. Очевидно, что на каждом элементе 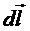вектор имеет свое направление и величину. Если кривая L замкнута, интегрирование ведется по замкнутому контуру, что обозначается кружком у знака интеграла, а интеграл от вектора носит название циркуляции вдоль контура L:

,

(1.4)

где b_l есть проекция вектора на соответствующий элемент контура.

Положим теперь, что контур L есть плоский прямоугольник (рис. 1.4), имеющий стороны Dx и Dy. Выбрав обозначенное стрелкой направление обхода, начатого из точки А, получим возможность представить означенный выше интеграл суммой четырех произведений, взятых последовательно по каждой из сторон:

,

(1.5)

где — значения проекций вектора на соответствующие стороны прямоугольника. Отрицательный знак появляется потому, что обход по контуру дважды совпадает с убылью координаты. Условимся выбирать прямоугольник столь малым, чтобы на его сторонах Dx и Dy соответствующие проекции вектора можно было бы считать постоянными. Последнее означает, что при обходе, например, по стороне Dy проекция b_y сохраняет свое значение, но проекция b_x будет меняться. При обходе по Dx, естественно, меняться будет проекция b_y. Изменение проекции b_y на единицу пути по оси x составит , а изменение b_x на единицу пути по оси y — . Значения b_y, например, на отрезках AD и BC будут отличаться друг от друга на величину . Следовательно

; .

(1.6)

Тогда

.

(1.7)

Раскрывая скобки и заменяя произведение DxDy через DS, получим:

.

(1.8)

Полученное выражение есть циркуляция вектора в двумерном случае.

3. Коснемся теперь еще одного понятия — градиента. Пусть имеется скалярное поле j, то есть заданные в каждой точке значения некоторой скалярной величины j. Выделим в нем совокупность точек, где значения функции j одинаковы (рис. 1.5) и равны какому-либо значению j₀. Эта совокупность образует поверхность, называемую поверхностью уровня. Рядом расположены поверхности с большими и меньшими значениями этой же скалярной величины. Выберем произвольное направление . Производная будет характеризовать изменение функции j на единицу длины в направлении . Теперь проведем к поверхности j₀ нормаль . Производная будет также характеризовать изменение этой же функции j на единицу длины, но уже в направлении . Естественно, значения производных не будут одинаковы: производная по n больше производной по l.

Вектор, численно равный и направленный по нормали к поверхности уровня, называют градиентом скалярной функции j:

grad.

(1.9)

Очевидно, что производная от j по направлению l равна проекции вектора градиента на это направление, так как ¶n = ¶lcosa (см. рис. 1.5). Отсюда можно заключить, что в направлении вектора градиента значение функции j меняется наиболее быстро: при положительном значении градиента — возрастает, при отрицательном — уменьшается.

В декартовых координатах градиент можно представить как векторную сумму его проекций на оси координат:

grad

(1.10)