4.1. Кинематика гармонических колебаний
Отличительной чертой колебательного движения является его периодичность, повторяемость. При этом движении существенно отличие пройденного пути, который постепенно растёт, от смещения x из какого-либо начала отсчёта.
Это смещение при колебаниях тела периодически меняется.На рис. 4.1 изображено колеблющееся тело, в случае, когда в начальный момент времени t = 0 его отклонение от положения равновесия было максимальным: тело было оттянуто на величину xо = xm от положения равновесия, в котором оно
находилось в состоянии покоя, и пружина была растянута только под действием силы тяжести тела, а затем отпущено одновременно с включением секундомера.  Под действием силы упругости величина смещения начнет уменьшаться до x = 0 и затем по инерции возрастать в сторону отрицательных значений до x = – xm (пружина сжимается) и т.д. Через xm обозначено максимальное значение x, называемое амплитудой, поэтому xm часто заменяют на букву A.
Под действием силы упругости величина смещения начнет уменьшаться до x = 0 и затем по инерции возрастать в сторону отрицательных значений до x = – xm (пружина сжимается) и т.д. Через xm обозначено максимальное значение x, называемое амплитудой, поэтому xm часто заменяют на букву A.
Для выражения зависимости смещения от времени в рассмотренном случае удобнее всего принять функцию косинуса, введя под его знак постоянную  , которая должна иметь размерность с-1, чтобы под знаком косинуса стояла безразмерная величина:
, которая должна иметь размерность с-1, чтобы под знаком косинуса стояла безразмерная величина:
 . . | (4.1) |
Для случая, когда в начальный момент времени маятник находится в положении равновесия xо = 0, подошла бы функция синуса. В общем же виде пользуются соотношением, содержащим некоторый промежуточный параметр 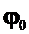 :
:
 . . | (4.2) |
В этом случае при t = 0 тело может находиться где-то в промежуточной точке.
Придавая разные значения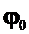 , можно приспосабливать (4.2) к конкретным начальным условиям колебания. Очевидно, что максимальное значение смещения в (4.1) и (4.2) будет равно амплитуде A, поскольку максимальное значение упомянутых выше функций равно единице.
, можно приспосабливать (4.2) к конкретным начальным условиям колебания. Очевидно, что максимальное значение смещения в (4.1) и (4.2) будет равно амплитуде A, поскольку максимальное значение упомянутых выше функций равно единице. Выясним смысл параметра  , воспользовавшись (4.1): очевидно, что смещение повторяется через определённые промежутки времени. Назовём периодом T время одного полного колебания. Через каждые T секунд тело возвращается в прежнее положение, то есть x принимает ранее имевшееся значение:
, воспользовавшись (4.1): очевидно, что смещение повторяется через определённые промежутки времени. Назовём периодом T время одного полного колебания. Через каждые T секунд тело возвращается в прежнее положение, то есть x принимает ранее имевшееся значение:
 , , | (4.3) |
следовательно,
 . . | (4.4) |
Поскольку значение косинуса повторяется при изменении угла на 2p, то
w(t+T) – wt = 2p и
 . . | (4.5) |
Циклическая частота w, введённая в (4.1), оказывается связанной с периодом.
Выражения, стоящие под знаком тригонометрических функций, показывают, какую часть от амплитуды составляет смещение и носят название фазы колебаний. Естественно, фаза – величина безразмерная. Величина  в (4.2) называется начальной фазой, она имеет тот же смысл, что и фаза колебания для момента времени t = 0.
в (4.2) называется начальной фазой, она имеет тот же смысл, что и фаза колебания для момента времени t = 0.
Таким образом, описывая колебательное движение, мы можем пользоваться любой периодической функцией, введя в уравнение колебаний три постоянные величины (параметры): амплитуду, начальную фазу, циклическую частоту. Смещение из положения равновесия остается функцией только одной переменной – времени.
Скорость колеблющегося тела найдётся как первая производная от смещения, а ускорение – как вторая производная:
 ; ;
| (4.6) |
Интересно, что ускорение будет отрицательным и в случае, если движение описывается уравнением (4.2).
Смысл этого понятен: ускорение всегда направлено в сторону, противоположную смещению, то есть к положению равновесия тела. Безусловно, без выполнения этого положения не было бы колебаний.Следует заметить, что колебательное движение не будет равноускоренным: ускорение есть функция времени. График зависимости a(t) будет синусоидой, так же как и график зависимости смещения от времени x(t) (рис. 4.2).
|
Очень полезно познакомиться и с геометрическим способом изображения колебательного движения – векторной диаграммой (рис. 4.3). Вектор, длина которого равна амплитуде и не меняется с течением времени, построен так, что составляет угол j с опорной осью. Опорная ось имеет произвольное направление и не обязательно горизонтальна. Угол  равен фазе колебания, и смещение x из положения равновесия будет проекцией вектора
равен фазе колебания, и смещение x из положения равновесия будет проекцией вектора  на опорную ось.
на опорную ось.
С течением времени фаза  растет, значит вектор будет вращаться вокруг своего начала с угловой скоростью w, а проекция при этом будет периодически меняться. Если фаза колебаний задана полностью, с начальной фазой
растет, значит вектор будет вращаться вокруг своего начала с угловой скоростью w, а проекция при этом будет периодически меняться. Если фаза колебаний задана полностью, с начальной фазой  , как в (4.2), диаграмму можно построить и для случая
, как в (4.2), диаграмму можно построить и для случая  . Тогда угол между опорной осью и амплитудой будет равен
. Тогда угол между опорной осью и амплитудой будет равен  . Изложенный выше геометрический способ представления колебаний иногда очень удобен, например при сложении одинаково направленных колебаний.
. Изложенный выше геометрический способ представления колебаний иногда очень удобен, например при сложении одинаково направленных колебаний.
 .
.
