2.8. Эквипотенциальные поверхности. Вычисление потенциала
Равенство (2.51) занимает в электростатике особое место, поэтому есть смысл обсудить его подробнее. Прежде всего, оно служит основанием для того, чтобы определять характер изменения потенциала по ходу силовых линий, которые, как мы уже успели заметить, всегда начинаются на положительных зарядах.
Нетрудно показать, что по силовым линиям можно представить и форму поверхностей уровня, или поверхностей равного потенциала (см. 1.1, п. 3). Эти поверхности (j = const) называют эквипотенциальными. Они всегда перпендикулярны силовым линиям. Покажем это.
Пусть заряд перемещается в поле отрицательно заряженного шара по элементу траектории 
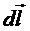(рис. 2.14). Работа по перемещению заряда может быть найдена двумя способами: по напряжённости (2.48) и по изменению потенциала (2.46). Приравняем правые части этих равенств:
| Eqdlcosα = qdφ | (2.52) |
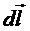— элемент эквипотенциальной поверхности, то dφ = 0 в силу постоянства на ней потенциала. В левой части равенства в нуль может обратиться лишь косинус, если угол между силой 
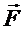и перемещением 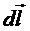будет прямым. Значит, эквипотенциальные поверхности должны быть перпендикулярны силовым линиям, по которым направлена напряженность. Для взятого в качестве примера поля заряженного шара эквипотенциальные поверхности будут концентрическими сферами, потенциал которых убывает по мере приближения к шару (потенциал убывает в направлении силовых линий). В разделе 1.1, посвященном элементам векторной алгебры, было введено понятие градиента, как вектора, направленного по нормали к эквипотенциальной поверхности и показывающего направление максимального возрастания скалярной величины. В (2.51) dl, равное dr, взято по силовой линии, т.е. перпендикулярно эквипотенциальной поверхности. Значит, напряженность следует считать градиентом потенциала, взятым с обратным знаком. Иначе: вектор напряженности показывает направление максимальной убыли потенциала. Естественно, рассматривая трехмерный случай, можно напряженность представить в виде суммы проекций (1.10). Прежде, чем перейти к расчёту потенциала или полей различных зарядов, уместно подвести некоторый итог: электростатическое поле имеет всего две характеристики: силовую (напряженность) и энергетическую (потенциал). Знание любой из них позволяет рассчитать работу по перенесению заряда в поле. Если к перечисленным выше физическим величинам добавить еще силу и энергию, то мы получим весь спектр величин, входящих в задачи по электростатике. Все они связаны друг с другом и вычисляются одна через другую. Но эта связь несколько иная для случая, когда поле создано точечным зарядом, по сравнению с той, когда заряд, создающий поле, нанесен на тело любой другой формы. В первом случае можно пользоваться законом Кулона, во втором — прямое его использование исключается. Попытаемся проиллюстрировать эту разницу двумя схемами, показывающими связь перечисленных величин для двух случаев. Каждый последующий член в этих схемах вычисляется через предыдущий. Обратим внимание не только на различие этих случаев, но и на положение потенциала на каждой из приведённых ниже схем. Для полей точечных зарядов последовательность расчёта физических величин через заряд Q, создающий поле, такова:
,
| (2.53) |
и для поля, созданного зарядом любой формы:
 | (2.54) |
Разница в нахождении напряженности в этих двух случаях очевидна, так же как и тот факт, что потенциал поля любого заряда может быть найден только через напряженность интегрированием уравнения (2.51).
Рассмотрим, как это делается на конкретных примерах.
Пример 1. Пусть задана положительно заряженная сфера радиуса R0, с поверхностной плотностью зарядов σ. Требуется найти потенциал поля в точке, расположенной на расстоянии R1 от её центра (рис. 2.15). Интегрируем (2.51), записанное с точностью до знака (ведь знак определяет направление изменения потенциала, а оно нам будет известно по ходу силовых линий, указанных на рисунке):
 . | (2.55) |
Поясним, как были выбраны пределы интегрирования: в задаче требуется найти не разность потенциалов, а потенциал, поэтому нижний предел в левой части равен нулю. Соответственно в правой части, где интегрирование ведётся по переменной r, нижний предел равен бесконечности, так как потенциал обращается в ноль там, где нет поля. Стоящая под интегралом напряжённость не постоянна, меняется при изменении расстояния r от центра сферы, поэтому, прежде чем приступить к интегрированию, её следует выразить в функции этого расстояния.
Задача нахождения потенциала свелась к нахождению напряжённости. Такая ситуация является общей для полей, созданных зарядами любой формы. Напряжённость необходимо находить каждый раз соответственно форме заряда, заданного в задаче. Поскольку в рассматриваемом случае заряд не точечный, будем следовать схеме (2.54) и искать напряжённость через её поток Ф. Последний может быть найден по теореме Гаусса. Заряд и силовые линии поля изображены на рис. 2.15. Здесь же пунктиром проведена вспомогательная поверхность — сфера произвольного радиуса r, заключающая внутри себя заряды, создающие поле. Заметим, что она не проходит через заданную точку поля R1, а имеет радиус, величина которого лежит между пределами, указанными в (2.55). Дело в том, что мы ищем напряжённость не в точке R1.
Найденное нами выражение для напряжённости пойдёт под интеграл и, следовательно, радиус поверхности не должен быть фиксированным, тогда и напряжённость будет выражена в функции переменного радиуса, а не будет являться напряжённостью в фиксированной точке! Проведя поверхность, мы теперь можем записать теорему Гаусса, то есть определить полный поток через эту поверхность: . | (2.56) |
Выразив поток через напряжённость, по определению потока
| Ф = E(4pr2), | (2.57) |
и приравнивая потоки, получим значение напряжённости. Подставив его под интеграл, будем иметь
 . | (2.58)
|
Или окончательно:
 , | (2.59) |
где φ1 — потенциал в точке, находящейся на расстоянии R1 от центра заряженной сферы. С увеличением этого расстояния потенциал уменьшается.
Решение легко использовать для нахождения потенциала в точках, лежащих на самой заряженной поверхности. В этом случае изменится лишь верхний предел в правой части интегралов (2.55) и (2.58), что приведёт к замене в выражении для потенциала R1 на R0. Потенциал на поверхности заряженной сферы оказывается величиной постоянной.
Для вычисления потенциала внутри заряженной сферы вспомогательную поверхность следует проводить через любую точку, отстоящую от центра на расстояние R2 < R0. Поскольку она не будет внутри себя содержать заряд, поток Ф будет равен нулю, и уравнение (2.57) даёт такой результат:
| E(4πr2)= 0; ? Е = 0, | (2.60) |
т.е. напряжённость внутри заряженной сферы равна нулю.
Потенциал, связанный с ней равенством (2.51), будет постоянен по всей сфере радиуса R0 и равен потенциалу на поверхности сферы. На рис. 2.15 приведён график зависимости потенциала от расстояния: от 0 до R0 он не меняется, а начиная с r = R0 убывает с увеличением расстояния от центра сферы по уравнению (2.59).
Пример 2. Пусть задано теперь однородное поле, напряжённость которого равна E. Требуется найти напряжение между двумя точками этого поля, находящимися на расстоянии l друг от друга (рис. 2.16).
Вдоль силовых линий показана ось r. Как и прежде, задача решается интегрированием (2.51), записанным с точностью до знака:
 ; ? j2 – j1 = Е(r2 – r1). | (2.61) |
Разность потенциалов и есть искомое напряжение. В силу постоянства напряжённости решение задачи не потребовало нахождения её значения, она была вынесена за интеграл. Разность координат r2 и r1 может быть заменена через d, и тогда получится известная из школьного курса физики формула:
| U = Ed. | (2.62) |
При необходимости вместо d можно ввести l, если известен угол α.