Позиционирование робота относительно визуальных ориентиров
а). Вычисление местоположения по одному ориентиру
Обнаружив один ориентир, робот уже может сделать оценку своего текущего местоположения. Каждый обнаруженный ориентир Їописывается вычисленными с некоторой точностью координатами в системе координат робота 
и принадлежит некоторому классу ориентиров Lk.
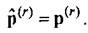Знание класса ориентира позволяет сократить число совпадающих с Їориентиров до Nk. Положение ориентиров в системе координат робота удобно представлять в полярных координатах 
где г - обозначает расстояние от робота до ориентира, аг- обозначает азимут обнаруженного ориентира в локальной системе координат робота.
Для любого ориентира
на карте с глобальными координатами
, совпадающего с обнаруженным роботом ориентиром
имеющего относительные координаты
все возможные местоположения робота
лежат на окружности, заданной уравнением (см. рис.4.5).
I
где угол а используется для вычисления ориентации робота для конкретной точки окружности при помощи выражения
Рис.4.5.
Вычисление местоположения робота по обнаруженному ориентиру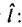
а - один ориентир; б - несколько ориентиров Рис.4.5 показывает основные геометрические соотношения, используемые для вычисления возможного положения робота (г - азимут обнаруженного ориентира в CK робота). Робот может находиться на любой точке окружности, заданной уравнением (4.21). На рис.4.5,б показаны все возможные положения робота для случая, если карта содержит несколько ориентиров того же типа, что и обнаруженный. Здесь видно, что в случае глобальной неопределенности местоположения, обнаружение даже одного ориентира может значительно уточнить информацию о позиции робота. Если же неопределенность о текущем положении невелика, то обнаружение только одного ориентира может уменьшить ее и даже позволить получить однозначное решение. Следует отметить, что на рис.4.5,б изображен наихудший случай локализации по одному ориентиру, когда все ориентиры на карте рабочего пространства одного класса. Очевидно, что если на карте имеется несколько различимых классов ориентиров, то обнаружение одного ориентира определенного класса позволит получить намного лучшую оценку текущего местоположения робота.
б). Вычисление местоположения по нескольким ориентирам
Местоположение робота можно вычислить еще точнее при обнаружении двух ориентиров [305]. В данном случае используются методы триангуляции. Как и в предыдущем случае, пренебрежем погрешностями вычисления координат обнаруженных ориентиров
Для получения оценки текущего местоположения по двум обнаруженным ориентирам
во множестве ориентиров
карты L CJicjsyenнайти одну или более пар ориентиров
, подобных обнаруженной паре.
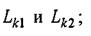
2) расстояние между обнаруженными ориентирами. Следует отметить, что для однозначного вычисления позиции двух ориентиров, как правило, недостаточно, если только не соблюдены определенные ограничивающие условия.
На рис.4.6 показаны все возможные решения задачи вычисления местоположения по двум обнаруженным ориентирам. Вычисленные координаты ориентиров
,обозначены
, соответственно. Следует упомянуть, что в
данном случае и расстояние до ориентиров и их азимуты являются важной информацией. Если известны только азимуты, то задача не имеет решения, так как робот может находиться на любой точке дуги, соединяющей ориентиры [206].
t
При знании только расстояний возможны четыре решения - точки
для подобных ориентиров и точки P1и P2для ориентиров других классов. Единственное решение для обнаруженных ориентиров может быть получено только, если известны расстояния и азимуты для обеих ориентиров, а также ориентиры относятся к разным классам. Если последнее условие не выполняется — обнаруженные ориентиры принадлежат к одному классу — то задача имеет два решения.
Найдем решение данной задачи для двух обнаруженных ориентиров разных классов. Оно находится в точке Pi.Введем вспомогательную систему координат
, начало которой совпадает с одним из обнаруженных ориентиров.
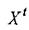вспомогательной системы координат идет в направлении второго ориентира и проходит сквозь него. В данном случае мы полагаем, что в качестве опорного ориентира выбран ориентир
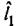(рис.4.7). На практике для этой цели должен быть выбран ориентир, координаты которого были вычислены с меньшей погрешностью.
где В - угол при вершине треугольника (см. рис.4.7), совпадающий с опорным ориентиром, который вычисляется по правилам триангуляции
где
угол между азимутами ориентиров. Знак
определяет знак В,
1
поэтому возможно исключить зеркальное решение в точке P1. Однако, данное зеркальное решение было бы действительным для случая двух обнаруженных ориентиров одного класса.
где
- глобальные координаты опорного ориентира ∕1, a β- угол
между осями Xвспомогательной и глобальной систем координат. Ориентация робота вычисляется по азимуту на опорный ориентир ж
220
Если ориентиры в паре
принадлежат одному классу, то существует еще
одно зеркальное решение в точке P2.Причина появления зеркального решения заключается в том, что ориентиры Z1и I2могут быть переставлены местами в паре.
В случае, когда ориентиры и робот находятся на одной прямой, r12= 0, но угол В может быть равен 0 или πв зависимости от знака разности rλ- r2.Как и в случае с одним ориентиром рассмотрим, как обнаружение двух ориентиров помогает роботу определить свое местоположение на глобальной карте, где могут присутствовать большое число подобных ориентиров. В случае глобальной неопределенности позиции два обнаруженных ориентира сократят количество всех возможных положений робота до небольшого множества возможных состояний. Размер данного множества будет зависеть от общего числа ориентиров и количества их классов. В случае локальной неопределенности два обнаруженных ориентира обычно позволяют точно определить действительное положение робота.
Для определения действительного местоположения робота в случае обнаружения роботом трех и более ориентиров, применяются обычные методы триангуляции [206,232,314].
4.3.