Постановка задачи и теоретические основы
В вероятностной локализации рабочее пространство робота представлено в виде пространства состояний Уверенность робота в его нахождении в состоянии ξ выражается функцией распределения плотности вероятности
Уверенность робота в его нахождении в состоянии ξ выражается функцией распределения плотности вероятности которая охватывает все возможные состояния робота в области
которая охватывает все возможные состояния робота в области

Чем выше значение для данного состояния ξ, тем выше вероятность, что робот действительно находится в этом месте.
для данного состояния ξ, тем выше вероятность, что робот действительно находится в этом месте.
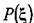 является функцией плотности распределения Дирака, где
является функцией плотности распределения Дирака, где 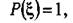 когда ξ выражает действительное местоположение робота, и
когда ξ выражает действительное местоположение робота, и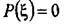 в
в другом случае. Если местоположение неизвестно, то функция плотности распре- делени? представляет собой равномерную функцию.
представляет собой равномерную функцию.
Для вычисления «действительного» местоположения робота по имеющемуся распределению плотности вероятности используют статистическую оценочную функцию.
В работе [374] приводятся два вида статистических оценочных функций, которые можно использовать в этих целях:• функция максимального правдоподобия (мода)

• оценочная функция Байеса (математическое ожидание)

Первая оценочная функция возвращает местоположение, имеющее максимальную вероятность. Если имеет несколько одинаковых максимумов, то случайным образом выбирается любой из них. Вторая оценочная функция находит взвешенное усредненное местоположение. Пусть
имеет несколько одинаковых максимумов, то случайным образом выбирается любой из них. Вторая оценочная функция находит взвешенное усредненное местоположение. Пусть обозначают
обозначают
серию из множеств ориентиров, последовательно наблюдаемых роботом во время своего функционирования, a tz1,tz2, ... обозначают серию действий (перемещений) робота на каждом из этих шагов. Без потери общности можно предположить, что обнаружение ориентиров камерой и передвижения робота следуют в последовательности друг за другом — сначала робот перемещается, затем происходит обнаружение им ориентиров. В вероятностных методах локализации [217,372,374], в основе которых лежит байесовский метод [321], местоположение робота на t-ом шаге выражается следующей функцией плотности вероятности
Следует заметить, что вычисление функции плотности вероятности после перемещения робота или обнаружения им ориентира подобно методу кал- мановской фильтрации [240], который состоит из двух основных фаз: фазы прогнозирования и фазы согласования.
после перемещения робота или обнаружения им ориентира подобно методу кал- мановской фильтрации [240], который состоит из двух основных фаз: фазы прогнозирования и фазы согласования.
Делая перемещение atна /-ом шаге, робот выполняет фазу прогнозирования.
Функция плотности вероятности местоположения обновляется при этом при помощи следующего рекурсивного выражения
где - функция плотности условной вероятности для перемещения
- функция плотности условной вероятности для перемещения
 местоположение робота до выполнения перемещения at.Функция
местоположение робота до выполнения перемещения at.Функция  определяет условную вероятность того, что совершая перемещение atмобильный робот изменит свое местоположение с
определяет условную вероятность того, что совершая перемещение atмобильный робот изменит свое местоположение с на ξ. Выражение (6.5) вычисляется для всех возможных местоположений робота
на ξ. Выражение (6.5) вычисляется для всех возможных местоположений робота
Когда робот на / -ом шаге обнаруживает серию ориентиров он выполняет фазу согласования своего прогноза с сенсорными данными
он выполняет фазу согласования своего прогноза с сенсорными данными Функция плотности вероятности местоположения обновляется по байесовской формуле
Функция плотности вероятности местоположения обновляется по байесовской формуле

Согласно Марковским предположениям (см. раздел 1.5.6), формула (6.6) примет следующий вид

где функция плотности вычисляется на основании используемой сен
вычисляется на основании используемой сен
сорной вероятностной модели рабочего пространства робота, а  байесовский знаменатель, используемый для нермирования интеграла по
байесовский знаменатель, используемый для нермирования интеграла по в (6.7).
в (6.7).
Таким образом, стандартный метод Марковской локализации может быть кратко представлен следующими шагами:
1. Инициализация: задается исходное распределение P(ξ0)∙
2. Для каждого перемещения atвычисляется рекурсивное выражение:

3. Для каждой наблюдаемой серии ориентиров Ltвычисляется следующее рекурсивное выражение:

При численной реализации метода функция плотности вероятности представляется в дискретном виде, а интегралы по области определения фукн- ции в указанных выше выражениях заменяются на операции суммирования по конечному числу состояний.
представляется в дискретном виде, а интегралы по области определения фукн- ции в указанных выше выражениях заменяются на операции суммирования по конечному числу состояний.
6.2.2.