Вычисление моментов инерции АТТ
Пример 1
Найдем момент инерции бесконечно круглого тонкого кольца (окружности). Момент инерции относительно оси Z (рис. 1), очевидно, равен
 , (1)
, (1)
где R – радиус кольца.
Ввиду симметрии Ix = Iy = 1∕2mR2.Формула (1), очевидно, дает также момент инерции полого однородного цилиндра с бесконечно тонкими стенками относительно его геометрической оси.

Рис. 1
Пример 2
Найдем момент инерции бесконечно тонкого диска. Предполагается, что диск однородный, т.е. вещество распределено в нем с постоянной плотностью. Пусть ось Z, проходит через центр диска С перпендикулярно к его плоскости (рис. 2). Рассмотрим бесконечно тонкое с внутренним радиусом r и наружным радиусом r+dr . Площадь такого кольца  . Его момент инерции найдется по формуле IZ = mR2. Момент инерции всего диска определяется интегралом
. Его момент инерции найдется по формуле IZ = mR2. Момент инерции всего диска определяется интегралом  . Ввиду однородности диска
. Ввиду однородности диска  , где
, где  - площадь всего диска. Вводя это выражение под знак интеграла, получим
- площадь всего диска. Вводя это выражение под знак интеграла, получим
 (2)
(2)
Момент инерции относительно диаметра вдвое меньше, как это непосредственно следует из формулы Ix + Iy = Iz , и из соображения симметрии:
 (3)
(3)

Рис. 2
Пример 3
Найдем момент инерции однородного цилиндра относительно его геометрической оси ОО.
Разобьем цилиндр на слои радиуса R и толщины dR. Масса такого слоя равна dm = ρ·dV = ρ·2πRh·dR (dV – объем слоя). Все точки слоя стоят от оси ОО на одинаковое расстояние R. Поэтому вклад слоя в момент инерции равен (4)
(4)
Проинтегрировав это выражение по R в пределах от 0 до r (r – радиус цилиндра), получим искомый момент инерции:
 (5),
(5),
где  - масса цилиндра. Отметим, что полученное выражение не зависит от высоты цилиндра h. Следовательно, формула (5) определяет и момент инерции тонкого диска относительно перпендикулярной к нему проходящей через его центр оси.
- масса цилиндра. Отметим, что полученное выражение не зависит от высоты цилиндра h. Следовательно, формула (5) определяет и момент инерции тонкого диска относительно перпендикулярной к нему проходящей через его центр оси.
Пример 4
Найдем момент инерции однородной тонкой палочки (прямого тонкого стержня) длиной l относительно центра. Разобьем палочку на одинаковые массы равные dm, возьмем dm, которая будет размещаться на отрезке dx. В формулу  можем подставить равные отношения
можем подставить равные отношения
 , (6)
, (6)
тогда получим  . Интегрируем выражение.
. Интегрируем выражение.
 . (7)
. (7)
Используя теорму Гюйгенса-Штейнера найдем момент инерции однородной палочки, если ось перпендикулярна и проходит через ее конец:
 (8)
(8)
Введем понятие Тензор инерции – матрица, в которой по диагонали располагаются моменты инерции АТТ (для симметричных тел)
 (9)
(9)
На месте Izz записывается максимальное значение момента инерции АТТ.
Разберемся на примере момента инерции кольца.
 (см. выше). Так как тело симметрично, то
(см. выше). Так как тело симметрично, то 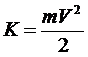 . Значит тензор инерции для кольца :
. Значит тензор инерции для кольца :
Если все 3 главных момента инерции равны, т.е.  , то тело называется сферическим волчком (шар, сфера…).
, то тело называется сферическим волчком (шар, сфера…).
Если  - симметричный волчок (кольцо, диск, цилиндр, конус…).
- симметричный волчок (кольцо, диск, цилиндр, конус…).
Если  - несимметричный волчок (параллелепипед).
- несимметричный волчок (параллелепипед).
Тензор инерции цилиндра  .
.
Приведем значения моментов инерции (табл. 1) для некоторых тел (тела считаются однородными, m - масса тела).
Таблица 1.Моменты инерции однородных тел простейшей формы относительно некоторых осей
| Тело | Положение оси | Момент инерции |
| Полый тонкостенный цилиндр радиусом R | Ось симметрии | mR2 |
| Сплошной цилиндр или диск радиусом R | Ось симметрии | 1∕2mR2 |
| Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через его середину | 1∕12ml2 |
| Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через его конец | 1∕3ml2 |
| Шар радиусом R | Ось проходит через центр шара | 2∕5mR2 |