Правило одновременной подстановки.
Замечание: Если формула 
выводима, то выводима и 
Возьмем формативную последовательность вывода 
и добавим в неё 
, получившаяся последовательность является формальным выводом.
(Если выводима 
то если 
, то выводима 
)
Теор: Если выводимая формула , то 
(
- различные символы переменных) выводима
Выберем 
- символы переменных которые различны между собой и не входят не в одну из формул 
, сделаем подстановку 
и последовательно применим 
и в новом слове делаем последовательную подстановку: 
, где 
- является формальным выводом.
3.1.3 Формальный вывод из гипотез.
Опр: Формальным выводом из гипотез 
(формулы), называется такая последовательность слов 
, каждая из которых удовлетворяет условию:
если формулу можно включить в некоторый формальный вывод из гипотез .
Лемма: ; 
: то тогда 
Напишем список:
Лемма:
Док: 
3.1.4 Теорема Дедукции.
Если из
1) и 2а) 
, где 
по правилу m.p.
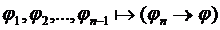, ч.т.д. 2б) 
- уже выводили 
, ч.т.д.
Базис индукции: N=1 
- формальный вывод из длинного списка
(только что доказано), осуществим переход по индукции:
по индукции
и по лемме 2
Пример: 
по теореме дедукции 