1.9.3. Функциональная полнота
Класс функций F называется полным, если его замыкание совпадает с Pn:
.
Другими словами, множество функций F образует полную систему, если любая функция реализуема в виде формулы над F.
Теорема.
Пусть заданы две системы функций 
и 
.
Тогда, если система F – полная и все функции из F реализуемы формулами над G, то система G тоже полная.
Доказательство. Пусть h – произвольная функция, 
. Тогда [F]=Pn, следовательно, h реализуема формулой 
, базисом которой является F (
). Если выполнить замену подформулы fi на подформулу 
в формуле , то мы получим формулу над G.
Следовательно, функция h реализуется формулой 
.
Примеры:
1. Система {
} – полная, т. к. любая логическая операция может быть выражена через дизъюнкцию, конъюнкцию и отрицание;
2. Система {
} – полная, т. к. 
3. Система {
} – полная, т.
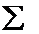
4. Система {|} – полная, т. к. 
, а {}и{} – полные системы.
5. Система {
} – полная, т. к. 
Представление логической операции системой{}называется полиномом Жегалкина. Таким образом, всякая логическая операция представима в виде
где 
- сложение по модулю 2, знак · обозначает конъюнкцию, 
.
Теорема Поста: Система логических операций полна тогда и только тогда, когда она содержит хотя бы одну функцию, не сохраняющую 0, одну функцию, не сохраняющую 1, хотя бы одну несамодвойственную функцию, хотя бы одну нелинейную функцию и хотя бы одну немонотонную функцию.
Пример.
Докажем полноту системы {A,U,1}.
| f | T0 | T1 | T* | TL | TM | В каждом столбце должен быть хотя бы один «-» |
| xAy | + | - | - | + | - | |
| xUy | + | + | - | - | + | |
| 1 | - | + | - | + | + |
1.
Проверка на принадлежность классу T0.
2.
Проверка на принадлежность классу T1.
3.
Проверка на принадлежность классу T*.
4.
Проверка на принадлежность классу TL.
5.
Проверка на принадлежность классу TM.
f(0,0)=0
f(0,1)=1
f(1,0)=1
f(1,1)=0
f(0,0)=0
f(0,1)=1
f(1,0)=1
f(1,1)=1
