Уравнение Лапласа
Будем выводить его неправильно, так, как выводил его сам Лаплас:
Ньютон вывел закон всемирного тяготения 
(
на единицу массы).
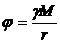, где r – расстояние между точкой с координатами (x0,y0,z0) где расположена масса M, и точкой наблюдения с координатами (x,y,z). 
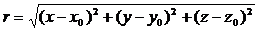. Далее Лаплас нашел, что с помощью этой субстанции можно вычислить проекции силы 
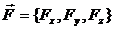, если вычислять ее по формуле 
, 
, 
точно также запишем
, 
.
В дальнейшем Лаплас предложил пользоваться не самим выражением для потенциала, а тем дифференциальным уравнением, которому оно удовлетворяет.
Получим это д. у.:Вычислим сначала вторую производную от потенциала по x:
, аналогично
, 
.
Складывая эти три частные производные, получаем уравнение Лапласа
(1)
Исторически это было первое уравнение с частными производными полученное математиками. Хотя уравнение Лапласа было получено для потенциала тяготения, оно описывает распределение большого количества совершенно различных физических величин, в частности уравнению (1) подчиняется потенциал электростатического поля, безвихревого течения идеальной жидкости, стационарное распределение концентрации в диффузионном поле или распределение температур.
В двухмерном случае уравнение Лапласа принимает вид
тогда говорят о плоской постановке задачи.